4. Dati, informazione e conoscenza
“Considerate la vostra semenza:fatti non foste a viver come bruti,ma per seguir virtute e canoscenza.”(Dante Alighieri, Inferno, canto XXVI) “Dove è la sapienza che abbiamo smarrito nella conoscenza,dove è la conoscenza che abbiamo smarrito nell’informazione,dove è l’informazione che abbiamo smarrito nei dati,dove sono i dati che abbiamo smarrito nel rumore.”(Anonimo) Il primo dei due fattori chiave per “la qualità della conoscenza” è rappresentato dalla qualità dell’informazione: che ci deve essere, deve essere giusta e deve essere completa. Ma cosa è l’informazione? La risposta a questa domanda si rivelerà cruciale. Letta dall’alto verso il basso la frase motto del sito può essere intesa come la metafora della società moderna. I ritmi di vita sempre più serrati, hanno prima rotto (per sempre?) quell’armonico senso di unità tra corpo, spirito e natura che gli antichi definivano sapienza. Quindi hanno imposto (e stanno sempre più imponendo) la necessità di suddividere l’enorme quantità di conoscenza globalmente disponibile, in sottoinsiemi (ecco che nasce la figura dello specialista) di dimensioni compatibili con la limitatezza della capacità di gestione della nostra mente (la corteccia cerebrale umana, sebbene incredibilmente complessa e sofisticata, possiede un limite fisico finito, invalicabile). Ancora, i ritmi di vita sempre più serrati hanno imposto (stanno sempre più imponendo) la necessità di comprimere i processi di comunicazione. Il paradigma è rappresentato dalla comunicazione mediante immagini. Il processo di comunicazione aumenta in efficienza [a], e aumenta in efficacia [b]. Ma la comunicazione mediante immagini, a fronte di un aumento dell’efficienza e dell’efficacia del processo di comunicazione, comporta anche una perdita del dettaglio [c]. Inoltre il messaggio “visivo” ricevuto viene tendenzialmente percepito come compiuto: la società dell’immagine spinge quindi anche a fare perdere il valore aggiunto determinato dalla riflessione/analisi critica dell’individuo sul suo contenuto. La conoscenza ha ormai lasciato il posto all’informazione. L’informazione fatta non per informare, ma fine a sé stessa, l’informazione-business, è il grande fratello orwelliano già presente tra noi (ma quanti se ne sono accorti?). Ma c’è di peggio nell’aria. Il flusso informativo è talmente imponente, rispetto al tempo dedicato/dedicabile alla riflessione critica su di esso da parte del singolo individuo, da rischiare di diventare semplicemente un flusso di dati. E infine come fare, nella società dell’informazione, a riconoscere gli elementi significativi, i dati, dal rumore di fondo? (in alternativa qualcuno ha già proposto “dove sono i dati, che abbiamo smarrito nel web?”: un problema reale, tanto che si sta cercando di affrontarlo con il progetto per un web semantico). Poichè qui dobbiamo peraltro circoscrivere il tema, riflettiamo sul passaggio (leggendo la frase dal basso verso l’alto) dati → informazione → conoscenza limitandoci (si fa per dire) a discutere della complessità dei processi che consentono di trasformare i dati di laboratorio in informazione utile dal punto di vista medico e quindi in conoscenza dello stato di salute del paziente. Prima di continuare vale la pena di ricordare le definizioni di dato, informazione e conoscenza fornite da un noto vocabolario [1]:→ Dato: elemento o serie di elementi accertati e verificati che possono formare oggetto di indagini, ricerche, elaborazioni o che comunque consentono di giungere a determinate conclusioni.→ Informazione: atto, effetto dell’informare o dell’informarsi, essendo a sua volta... → informare: modellare secondo una forma.→ Conoscenza: facoltà, atto, modo, effetto del conoscere, essendo a sua volta... → conoscere: prendere possesso intellettualmente o psicologicamente, specialmente con un’attività sistematica, di qualunque aspetto di quella che è considerata realtà. La corrispondenza tra i diversi stati attraversati dalle rappresentazioni mentali sulla via dell’intelligere (dati → informazione → conoscenza) e le azioni da cui essi derivano è la seguente:
DATI → informazione → conoscenza Il dato è la prima rappresentazione mentale, quella più elementare: ma è già di per sé una grande conquista intellettuale. Il dato è il risultato di un processo di astrazione. Fornire una tabella che riporta l‘altezza in centimetri di 1000 soggetti appartenenti alla popolazione italiana, corrisponde a fornire un elenco di dati. Dove “l’altezza in centimetri” è il risultato “concreto” di un procedimento di misura “astratto”. Data la sua importanza, una breve introduzione all’argomento metrologico è riportata nell’appendice A. Ci ricorda l’importanza straordinaria della misura Robert Laughlin, premio Nobel per la fisica nel 1998 con Daniel C. Tsui e Horst Störmer per la scoperta dell’effetto Hall quantistico. Dice Laughlin [2]: “…misurando con una precisione di una parte su centomila, scopriamo che la lunghezza di un mattone varia da un giorno all’altro. Analizzando i fattori ambientali, scopriamo che ciò è dovuto alle variazioni di temperatura, che determinano infinitesimali contrazioni ed espansioni del mattone. Il mattone si comporta quindi come un termometro. Non si tratta affatto di un’osservazione sciocca, dal momento che la dilatazione termica è il principio alla base di qualsiasi comune termometro. Misurando il peso con analoga precisione, non si registra alcuna variazione, ed è proprio questa una delle osservazioni che portano al principio di conservazione della massa. Se peraltro lavoriamo con una precisione di una parte su cento milioni, il peso del mattone potrà variare leggermente da un laboratorio all’altro. A questo punto, il nostro mattone è diventato un misuratore di gravità, trattandosi dell’effetto di minuscole variazioni della forza di gravità, dovute alla diversa densità delle rocce che giacciono immediatamente sotto la superficie terrestre…” L’esperienza ha mostrato che nessuna misura, per quanto effettuata con cura, può essere completamente libera da errori [3]. E’ a Karl Friedrich Gauss, “il principe dei matematici” che dobbiamo la formalizzazione matematica dell’errore di misura, un prerequisito essenziale per calcolare l’incertezza globale delle nostre conclusioni al termine del procedimento di misura (per i concetti minimi sull’errore di misura e sulla sua espressione si rimanda all’appendice B). Ci siamo preoccupando del fatto che i dati, come prerequisito dell’informazione, poggino su solide fondamenta. La teoria, dopo avere dimostrato che i nostri dati sono inevitabilmente incerti, ci consente almeno di quantificare in modo oggettivo tale incertezza, di misurarla. Eccoci quindi ai due opposti, che riflettono l’ambivalenza di tutte le cose umane. Senza misure non si può fare scienza. Ma cullarsi in una sorta di “illusoria certezza dei numeri” è altrettanto sbagliato. L’incertezza fa parte strutturale della conoscenza. Il segreto consiste nel gestirla al meglio. dati → INFORMAZIONE → conoscenza Il problema diventa assai più complesso quando passiamo dai dati all’informazione: perché informare, come abbiamo detto, significa dare forma, e questo aspetto mal si presta ad una analisi quantitativa. Per affrontare il “dare forma ai dati” secondo regole scientifiche abbiamo l’esigenza di avere strumenti di modellazione del dato rigorosi e neutrali. Abbiamo detto che fornire una tabella che riporta l‘altezza in centimetri di 1000 soggetti appartenenti alla popolazione italiana, corrisponde a fornire un elenco di dati. Dire che “l’altezza media, in un campione rappresentativo di 1000 italiani, è di 168,4 centimetri” corrisponde a dare un’informazione. Ma chi ha dato forma ai dati? E in che modo ha dato forma ai dati? Ovviamente questo apre una questione assai spinosa. PROBLEMA 5Supponiamo di avere determinato la concentrazione nel siero dei trigliceridi (espressi in mg/dL) in 1000 soggetti, scelti a caso tra i pazienti che effettuano ambulatoriamente analisi di laboratorio. I risultati sono riportati nella tabella dell’appendice C. Dopo avere analizzato statisticamente i dati, riassumiamo le conclusioni che abbiamo attenuto a un nostro amico, comunicandogli questa informazione: “abbiamo verificato che in 1000 soggetti, scelti a caso tra i pazienti che effettuano ambulatoriamente analisi di laboratorio, la concentrazione media dei trigliceridi era 136.509 mg/dL, con una deviazione standard (ds) di 92.76759 mg/dL”.Quale conclusione il nostro amico può dedurre dai dati che gli abbbiamo fornito? Il nostro amico, dall’informazione che gli abbiamo fornito, e rammentando che in base alle proprietà della distribuzione gaussiana tra la media - 1,96 d.s. e la media + 1,96 d.s. si deve trova il 95% dei dati campionari, rispettivamente sottrae e aggiunge alla media 181,8144764 mg/dL (cioè 1,96 · 92.76759 mg/dL) e ottiene rispettivamente, dopo arrotondamento alla prima cifra decimale, -45,3 mg/dL e 318,3 mg/dL. Dal che il nostro amico deduce che una certa quota dei pazienti aveva valori negativi della concentrazione nel siero dei trigliceridi! Tuttavia, prima di pubblicare questa rivoluzionaria conclusione, la prudenza impone un riesame dei risultati effettivamente ottenuti (tabella dell’appendice C): e il riesame dei dati dimostra che nessuno dei valori era inferiore a zero. Un evidente paradosso biologico (una concentrazione negativa) non porta ad una rivoluzionaria conclusione, ma più semplicemente consente di individuare un grave errore nel dare forma ai dati: calcolando media e deviazione standard è stata (implicitamente) data forma gaussiana a dati che non sono distribuiti in modo gaussiano. Per illustrare ulteriormente le implicazioni del “dare forma ai dati” vediamo un secondo esempio, un pò più tecnico, ma molto istruttivo. Esistono numerose occasioni nelle quali quello che interessa è ricostruire la relazione di funzione che lega due variabili, la variabile y (variabile dipendente, in ordinate) alla variabile indipendente (variabile x, in ascisse); se si ritiene che la relazione esistente fra le due variabili possa essere convenientemente descritta mediante una retta, l'equazione di tale retta può essere calcolata mediante la tecnica statistica nota come regressione lineare. Tale denominazione deriva dagli studi sull'ereditarietà condotti da F. Galton sul finire dell'800. Nel corso di questi studi vennero, fra l'altro, registrate le altezze dei componenti di più di 1000 gruppi familiari. Ponendo su un sistema di assi cartesiani in ascisse le altezze dei padri e in ordinate le altezze dei figli, si notò un fatto: sebbene in genere padri più alti avessero figli più alti (come del resto era atteso), padri che erano di 16 centimetri circa più alti della media dei padri, avevano figli che erano solamente 8 centimetri circa più alti della media dei figli. In altre parole sembrava che vi fosse un "tornare indietro", una regressione delle altezze dei figli rispetto a quelle dei padri : e il termine che descriveva il risultato di questa iniziale applicazione, finì con l'essere impiegato per indicare la tecnica statistica, ed è rimasto ancora oggi nell'uso, anche se l’attributo di “regressione” non avrebbe più alcun significato di essere. PROBLEMA 6Si consideri il confronto tra due metodi analitici per la determinazione del calcio nel siero. Il confronto dà i seguenti risultati (concentrazione in milligrammi per decilitro di siero, mg/dL):
Quali conclusioni possono essere tratte dei risultati ottenuti? Ebbene, utilizzando tre diversi modelli di regressione lineare (appendice D), si ottengono i seguenti risultati: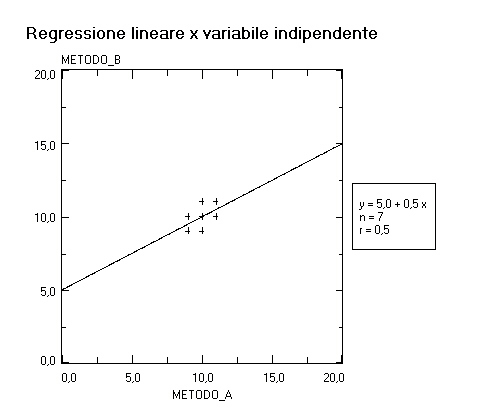 
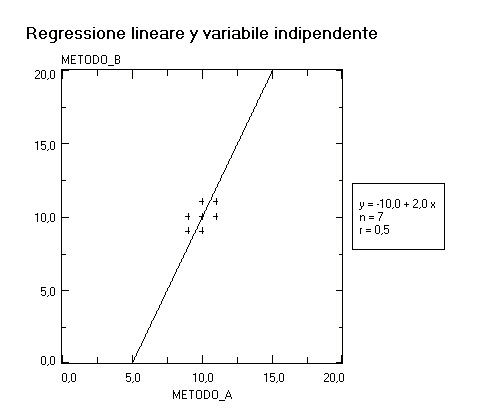
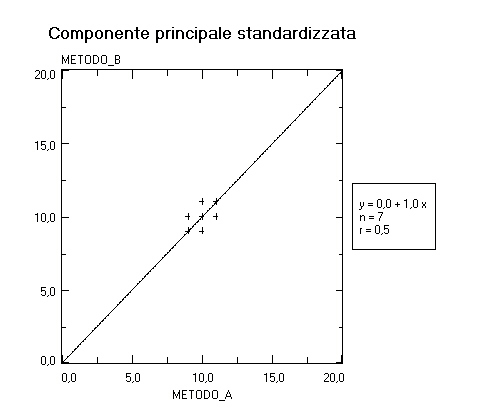Come è possibile che differenti modelli di regressione forniscano conclusioni così diverse? Quale modello fornisce i risultati più attendibili? Ebbene, gli assunti alla base dei modelli di regressione lineare utilizzati (x variabile indipendente, y variabile indipendente e componente principale standardizzata) sono identici, tranne che per il fatto che la regressione x variabile indipendente assume che la variabile in ascisse (x) sia la variabile misurata senza errore, la regressione y variabile indipendente assume che la variabile in ordinate (y) sia la variabile misurata senza errore, mentre la componente principale standardizzata assume che sia la variabile in ascisse sia la variabile in ordinate siano misurate con un errore dello stesso ordine di grandezza. La risposta alle due domande è che, nel caso specifico, il fatto che il coefficiente di correlazione r sia “solamente” 0,5 indica che l’informazione contenuta nei dati è troppo scarsa per fornire una indicazione univoca. In questo caso la forma che viene dati ai dati, e quindi la conclusione che da essi viene tratta, risulta determinata più dagli assunti del modello matematico (di regressione) che dal contenuto informativo dei dati stessi! Un terzo esempio è quello relativo all’espressione dei risultati di uno studio clinico controllato in termini di rischio o di rischio relativo (RR) [d]. Dal 19 al 23 marzo 2002 a Barcellona si è tenuto il 3rd European Breast Cancer Conference (EBCC-3). Dove sono stati presentati in maniera preliminare i dati di uno studio svolto su 103.000 donne norvegesi e svedesi, che ha dimostrato un lieve aumento del rischio di sviluppare un cancro della mammella con l’uso di contraccettivi orali (CO). I dati sono stati ripresi e pubblicati dalla stampa in un articolo, con grande clamore. Il messaggio è in sintesi che dopo cinque anni di assunzione di CO si ha un aumento del 26% di sviluppare un cancro della mammella. L’articolo comunica ovviamente una forte sensazione di allarme a chiunque lo legga. Ma vediamo di analizzare i dati. Innanzitutto la statistica sanitaria ci dice che sette donne su cento avranno un tumore al seno nel corso della loro esistenza. Questo è dunque il rischio basale (RR = 1,0) che ogni donna ha: sette probabilità su cento. In base i risultati dello studio queste donne passano da 7, nel gruppo che non assume CO, a 8,82 nel gruppo che assume CO (8,82/7 = 1,26). Quindi il messaggio è che, in valore assoluto, circa due donne su cento ammaleranno in più nel gruppo che assume CO. Ma questo è fondamentalmente diverso dal lasciare nella mente del lettore “il venticello” del 26% [e]. Quest’ultimo esempio si colloca in un’area che va dal “pregiudizio” del ricercatore, che compare nel momento in cui “da forma” ai dati in termini di rischio relativo, alla deformazione “propagandistica” di questi da parte del giornalista. I due precedenti esempi illustravano invece veri e propri “artefatti”. Ma la morale tutti e tre gli esempi sono accomunati da un problema soggiacente: dare forma ai dati è un fatto molto delicato, e la massima attenzione e il massimo scrupolo devono sempre guidare a questo proposito chi opera in campo scientifico [f]. dati → informazione → CONOSCENZA Il terzo elemento sulla via dell’intelligere, la conoscenza, intesa come “prendere possesso intellettualmente … della realtà [connettere]” ci ricollega al metodo di cartesiana memoria e al problema gnoeologico. La conoscenza scientifica non può essere di tipo esclusivamente deduttivo. Ma, seguendo le critiche all’induzione da Hume e K. Popper, non può nemmeno essere di tipo induttivo. Cerchiamo di riassumere queste due idee cruciali seguendo l’impostazione data da Charles S. Peirce. Come dice U. Volli [4] “... la struttura logica della deduzione [è la seguente]:REGOLA: Tutti i fagioli in questo sacco sono bianchiCASO: Questi fagioli provengono da questo saccoRISULTATO: Questi fagioli sono bianchi (sicuramente)... il ragionamento deduttivo non comporta alcun accrescimento del sapere. Noi sapevamo fin dall’inizio che i fagioli nel sacco erano bianchi, e ci siamo limitati a calcolare le conseguenze logiche di questo assunto: se estraiamo dei fagioli dal sacco, questi saranno necessariamente bianchi...” [4]. La deduzione è certa. Ma ne sappiamo quanto prima. “... la struttura logica dell’induzione [è la seguente]:CASO: Questi fagioli provengono da questo saccoRISULTATO: Questi fagioli sono bianchiREGOLA: Tutti i fagioli di questo sacco sono bianchi (probabilmente)... l’induzione ... ci consente di allargare orizzontalmente la nostra conoscenza del mondo. La sua essenza è la generalizzazione: noi immaginiamo che ciò che è vero per un certo campione preso a caso da un insieme sia vero anche per tutti gli altri componenti dell’insieme. Non ci vuole molta inventiva per compiere questo salto logico, che comunque è sempre passibile di errore...” [4]. L’induzione è sempre e solo probabile. Ma è un procedimento banale. Esiste tuttavia un modo alternativo di affrontare il problema, che passa “... attraverso la formulazione di ipotesi o abduzioni ...1) RISULTATO: Questi fagioli sono bianchi2) REGOLA: Tutti i fagioli di questo sacco sono bianchi3) CASO: Questi fagioli provengono da questo sacco (probabilmente)...” [4]. L’abduzione è sempre e solo probabile. Ma ci garantisce il valore aggiunto dell’immaginazione. E’ un procedimento creativo. Osservando "un fatto sorprendente" (abbiamo dei fagioli bianchi) e avendo a disposizione una regola in grado di spiegarlo (sappiamo che tutti i fagioli di questo sacco sono bianchi) possiamo ipotizzare che si dia il caso che questi fagioli vengano da questo sacco. In questo modo noi stiamo cercando di accrescere la nostra conoscenza. Cerchiamo di sapere qualcosa di più sui fagioli: prima sapevamo solo che erano bianchi, ora suppaniamo che provengano da questo sacco. L'abduzione, secondo Peirce, è l'unica forma di ragionamento suscettibile di accrescere il nostro sapere, in quanto permette di ipotizzare nuove idee, di indovinare, di prevedere. È altresì vero che l'abduzione è il modo inferenziale maggiormente soggetto a rischio di errore: l'abduzione, come l'induzione, non contiene in sé la sua validità logica, e deve essere confermata per via empirica [4]. Ecco che finalmente possiamo capire la frase di A. Einstein: “L’immaginazione è più importante della conoscenza” . Al vertice del pensiero scientifico sta l’ipotesi, ovvero la teoria: “l’immaginazione” nelle parole di Einstein, o ancora “l’abduzione” nella parole di Peirce. E’ questo il fatto veramente innovativo sul piano della conoscenza. L’esperimento viene concepito per verificare la teoria. Esperimenti che portano a risultati in accordo con la teoria ne aumentano la verosimiglianza (probabilità), anche se non ne potranno mai asserire la veridicità (verità). Esperimenti che portano ad osservazioni e conseguenze che non sono spiegabili con la teoria, sono in grado di confutarla (falsificarla) 
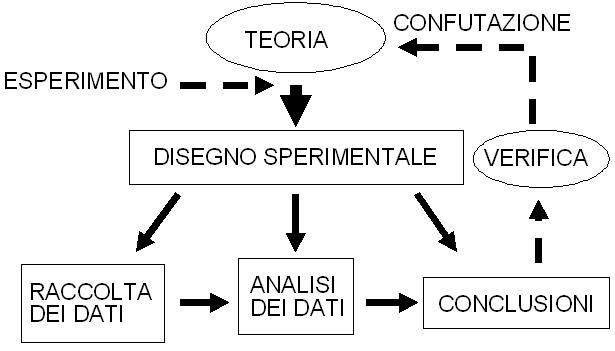Procede sempre nello stesso modo il “ricercatore”: che sia il fisico teorico che formula un’ipotesi sulla struttura della materia, che sia il medico che formula un’ipotesi sulla malattia del paziente, che sia il detective che formula un’ipotesi sul responsabile del delitto. Formula, appunto, un’ipotesi, e ne deduce delle conseguenze che sottopone a verifica sperimentale (empirica). Non è vero che il ricercatore non abbia un pregiudizio. Anzi paradossalmente lo deve avere. Perché è proprio l’immaginazione che innesca il ciclo del modello ipotetico-deduttivo, a sua volta motore, con l’esperimento, della conoscenza. Ed è l’accettazione “democratica” della verifica sperimentale che consente di accettare (provvisoriamente) o di rifiutare l’ipotesi. Generando una conoscenza mai certa, ma sempre creativa, aperta a nuove ipotesi, a nuove deduzioni, a nuove verifiche sperimentali, e per questo in grado di evolvere. ********************************
Come è possibile che differenti modelli di regressione forniscano conclusioni così diverse? Quale modello fornisce i risultati più attendibili? Ebbene, gli assunti alla base dei modelli di regressione lineare utilizzati (x variabile indipendente, y variabile indipendente e componente principale standardizzata) sono identici, tranne che per il fatto che la regressione x variabile indipendente assume che la variabile in ascisse (x) sia la variabile misurata senza errore, la regressione y variabile indipendente assume che la variabile in ordinate (y) sia la variabile misurata senza errore, mentre la componente principale standardizzata assume che sia la variabile in ascisse sia la variabile in ordinate siano misurate con un errore dello stesso ordine di grandezza. La risposta alle due domande è che, nel caso specifico, il fatto che il coefficiente di correlazione r sia “solamente” 0,5 indica che l’informazione contenuta nei dati è troppo scarsa per fornire una indicazione univoca. In questo caso la forma che viene dati ai dati, e quindi la conclusione che da essi viene tratta, risulta determinata più dagli assunti del modello matematico (di regressione) che dal contenuto informativo dei dati stessi! Un terzo esempio è quello relativo all’espressione dei risultati di uno studio clinico controllato in termini di rischio o di rischio relativo (RR) [d]. Dal 19 al 23 marzo 2002 a Barcellona si è tenuto il 3rd European Breast Cancer Conference (EBCC-3). Dove sono stati presentati in maniera preliminare i dati di uno studio svolto su 103.000 donne norvegesi e svedesi, che ha dimostrato un lieve aumento del rischio di sviluppare un cancro della mammella con l’uso di contraccettivi orali (CO). I dati sono stati ripresi e pubblicati dalla stampa in un articolo, con grande clamore. Il messaggio è in sintesi che dopo cinque anni di assunzione di CO si ha un aumento del 26% di sviluppare un cancro della mammella. L’articolo comunica ovviamente una forte sensazione di allarme a chiunque lo legga. Ma vediamo di analizzare i dati. Innanzitutto la statistica sanitaria ci dice che sette donne su cento avranno un tumore al seno nel corso della loro esistenza. Questo è dunque il rischio basale (RR = 1,0) che ogni donna ha: sette probabilità su cento. In base i risultati dello studio queste donne passano da 7, nel gruppo che non assume CO, a 8,82 nel gruppo che assume CO (8,82/7 = 1,26). Quindi il messaggio è che, in valore assoluto, circa due donne su cento ammaleranno in più nel gruppo che assume CO. Ma questo è fondamentalmente diverso dal lasciare nella mente del lettore “il venticello” del 26% [e]. Quest’ultimo esempio si colloca in un’area che va dal “pregiudizio” del ricercatore, che compare nel momento in cui “da forma” ai dati in termini di rischio relativo, alla deformazione “propagandistica” di questi da parte del giornalista. I due precedenti esempi illustravano invece veri e propri “artefatti”. Ma la morale tutti e tre gli esempi sono accomunati da un problema soggiacente: dare forma ai dati è un fatto molto delicato, e la massima attenzione e il massimo scrupolo devono sempre guidare a questo proposito chi opera in campo scientifico [f]. dati → informazione → CONOSCENZA Il terzo elemento sulla via dell’intelligere, la conoscenza, intesa come “prendere possesso intellettualmente … della realtà [connettere]” ci ricollega al metodo di cartesiana memoria e al problema gnoeologico. La conoscenza scientifica non può essere di tipo esclusivamente deduttivo. Ma, seguendo le critiche all’induzione da Hume e K. Popper, non può nemmeno essere di tipo induttivo. Cerchiamo di riassumere queste due idee cruciali seguendo l’impostazione data da Charles S. Peirce. Come dice U. Volli [4] “... la struttura logica della deduzione [è la seguente]:REGOLA: Tutti i fagioli in questo sacco sono bianchiCASO: Questi fagioli provengono da questo saccoRISULTATO: Questi fagioli sono bianchi (sicuramente)... il ragionamento deduttivo non comporta alcun accrescimento del sapere. Noi sapevamo fin dall’inizio che i fagioli nel sacco erano bianchi, e ci siamo limitati a calcolare le conseguenze logiche di questo assunto: se estraiamo dei fagioli dal sacco, questi saranno necessariamente bianchi...” [4]. La deduzione è certa. Ma ne sappiamo quanto prima. “... la struttura logica dell’induzione [è la seguente]:CASO: Questi fagioli provengono da questo saccoRISULTATO: Questi fagioli sono bianchiREGOLA: Tutti i fagioli di questo sacco sono bianchi (probabilmente)... l’induzione ... ci consente di allargare orizzontalmente la nostra conoscenza del mondo. La sua essenza è la generalizzazione: noi immaginiamo che ciò che è vero per un certo campione preso a caso da un insieme sia vero anche per tutti gli altri componenti dell’insieme. Non ci vuole molta inventiva per compiere questo salto logico, che comunque è sempre passibile di errore...” [4]. L’induzione è sempre e solo probabile. Ma è un procedimento banale. Esiste tuttavia un modo alternativo di affrontare il problema, che passa “... attraverso la formulazione di ipotesi o abduzioni ...1) RISULTATO: Questi fagioli sono bianchi2) REGOLA: Tutti i fagioli di questo sacco sono bianchi3) CASO: Questi fagioli provengono da questo sacco (probabilmente)...” [4]. L’abduzione è sempre e solo probabile. Ma ci garantisce il valore aggiunto dell’immaginazione. E’ un procedimento creativo. Osservando "un fatto sorprendente" (abbiamo dei fagioli bianchi) e avendo a disposizione una regola in grado di spiegarlo (sappiamo che tutti i fagioli di questo sacco sono bianchi) possiamo ipotizzare che si dia il caso che questi fagioli vengano da questo sacco. In questo modo noi stiamo cercando di accrescere la nostra conoscenza. Cerchiamo di sapere qualcosa di più sui fagioli: prima sapevamo solo che erano bianchi, ora suppaniamo che provengano da questo sacco. L'abduzione, secondo Peirce, è l'unica forma di ragionamento suscettibile di accrescere il nostro sapere, in quanto permette di ipotizzare nuove idee, di indovinare, di prevedere. È altresì vero che l'abduzione è il modo inferenziale maggiormente soggetto a rischio di errore: l'abduzione, come l'induzione, non contiene in sé la sua validità logica, e deve essere confermata per via empirica [4]. Ecco che finalmente possiamo capire la frase di A. Einstein: “L’immaginazione è più importante della conoscenza” . Al vertice del pensiero scientifico sta l’ipotesi, ovvero la teoria: “l’immaginazione” nelle parole di Einstein, o ancora “l’abduzione” nella parole di Peirce. E’ questo il fatto veramente innovativo sul piano della conoscenza. L’esperimento viene concepito per verificare la teoria. Esperimenti che portano a risultati in accordo con la teoria ne aumentano la verosimiglianza (probabilità), anche se non ne potranno mai asserire la veridicità (verità). Esperimenti che portano ad osservazioni e conseguenze che non sono spiegabili con la teoria, sono in grado di confutarla (falsificarla) Procede sempre nello stesso modo il “ricercatore”: che sia il fisico teorico che formula un’ipotesi sulla struttura della materia, che sia il medico che formula un’ipotesi sulla malattia del paziente, che sia il detective che formula un’ipotesi sul responsabile del delitto. Formula, appunto, un’ipotesi, e ne deduce delle conseguenze che sottopone a verifica sperimentale (empirica). Non è vero che il ricercatore non abbia un pregiudizio. Anzi paradossalmente lo deve avere. Perché è proprio l’immaginazione che innesca il ciclo del modello ipotetico-deduttivo, a sua volta motore, con l’esperimento, della conoscenza. Ed è l’accettazione “democratica” della verifica sperimentale che consente di accettare (provvisoriamente) o di rifiutare l’ipotesi. Generando una conoscenza mai certa, ma sempre creativa, aperta a nuove ipotesi, a nuove deduzioni, a nuove verifiche sperimentali, e per questo in grado di evolvere. ******************************** |
|
|
|
|
|
||
|
||
|
|
|
|
Ultimo aggiornamento: 20 febbraio 2023
NOTA SUI COLLEGAMENTIALLE FONTI BIBLIOGRAFICHE La maggior parte dei collegamenti ad articoli scientifici riportati nel sito fa riferimento a riviste online che forniscono gratuitamente l’articolo originale. In alcuni casi è necessario registrarsi sul sito per avere libero accesso agli articoli: questo accade per esempio con il BMJ. Quando i collegamenti fanno riferimento a fonti bibliografiche a pagamento, chi non ha sottoscritto un abbonamento con la rivista potrebbe vedere comparire un messaggio del tipo “access forbidden”, ma il più delle volte vedrà comparire una pagina che consente di acquistare online l’articolo originale.
scelti per voi
Programma di statistica Ministat (versione per Windows)
Programma di statistica Open Source R(per Linux, Mac OS X e Windows)
Manuale Merck di diagnosie terapia
L’articolo da non perdere...
Errori congeniti del metabolismo
I migliori libri del mese Leonard Mlodinow La passeggiata dell’ubriaco. Le leggi scientifiche del caso.Rizzoli Editore, 2009, pp. 294ISBN: 17034081
OpenOffice, la suite Open Source (per Linux, Mac OS X e Windows)
ebooks... Mauss, Berg, Rockstroh, Sarrazin, Wedemeyer.Hepatology - A clinical textbook. 10th Edition - 2020
Le lettureconsigliate
Atlante di anatomia del Bock
Tavole metaboliche
Informazioni: info@bayes.itScrivimi: webmaster@bayes.it
NOTA LEGALE L’interpretazione dei risultati delle analisi di laboratorio deve essere effettuata esclusivamente dal medico e alla luce dei dati clinici.Questo sito ha uno scopo esclusivamente educativo e formativo. Pertanto le informazioni in esso contenute possono essere utilizzate esclusivamente a scopo didattico, e anche in questo caso sotto la responsabilità personale di chi le utilizza, sia per sé stesso sia per terzi.Le informazioni contenute in questo sito non possono e non devono essere utilizzate né a scopo diagnostico, né a scopo prognostico, né a scopo terapeutico, né per qualsiasi attività che abbia un impatto sia diretto sia indiretto sullo stato di salute di un individuo o di più individui.Nessuna responsabilità può essere imputata all’autore per danni diretti o indiretti e di qualsivoglia natura che potrebbero essere causati a sé stessi o a terzi a causa di errori, imprecisioni, omissioni, interpretazioni o utilizzo dei contenuti di questo sito o dei siti cui esso fa riferimento.
E ora che i test genetici sono alla portata di tutti?Con meno di mille euro è possibile comprare un test genetico su Internet: si manda un piccolo campione di cellule e poi si aspetta la risposta. Ma... a che cosa serve la risposta? Un dossier di Marika De Acetis dall’Archivio storico del sito www.torinoscienza.it
[Home] [Errori cognitivi] [Epistemologia] [Teorema di Bayes] [Decisioni mediche] [Le basi biochimiche][Analisi tradizionali] [Analisi genetiche] [Qualità in laboratorio] [Statistica e laboratorio][Storia delle medicina] [Download] [Link] [Bacheca] [FAQ] [Chi sono]
Attualità in tema di eGFR:
I migliori libri del mese Giovanni Federspil Logica clinica. I principi del metodo in medicina.McGraw-Hill, 2004, pp. 368ISBN: 88 386 2984-6
Atlante di virologia
Dal settembre 2008oltre 400 000 visitatori
ebooks... M. BesozziErrori cognitivi, probabilità e decisioni mediche. Fate click sul titolo o scaricate il testo su tablet o smartphone con il codice a barre riportato qui sotto. 
Atlante dei protozoi intestinali
Atlante di citologia e istologia
Statistica e grafica con R
Espressione dei risultati nel laboratorio di chimica clinica
Pathology outlines
Atlante di anatomia del Gray
Atlante di ematologia
Atlante di parassitologia
Micobatteriologia clinica
Concetti, metodi e strumenti per una
buona informazione
ebooks... M. BesozziStatistica e grafica con R Fate click sul titolo o scaricate il testo su tablet o smartphone con il codice a barre riportato qui sotto. 
I migliori libri del mese Luigi Tesio I bravi e i buoni.Perché la medicina clinica può essere una scienza.Il Pensiero Scientifico Editore, 2015, pp. 216 ISBN: 978-88-490-0538-7
Gli inganni della correlazione:
Storia delle unità di misura
Questo sito è stato archiviato ed è reso disponibile esclusivamente come memoria storica: pertanto è escluso ogni suo possibile utilizzo medico. Le parti del sito riservate al teorema di Bayes rimangono concettualmente valide, ma declino qualsiasi responsabilità per la lenta ma inevitabile obsolescenza dei restanti contenuti dovuta alla comparsa di nuove analisi di laboratorio, di progressi nelle analisi genetiche, di link interrotti, e quant’altro.
.