“Ciò che gli uomini vogliono realmente non è la conoscenza, ma la certezza.”(Bertrand Russell) “Ci sono tre tipi di menzogne: le bugie, le bugie sfrontate, e le statistiche.”(Mark Twain) Per ridurre la componente di incertezza nelle decisioni mediche, oltre che utilizzare metodi di ragionamento “razionali”, è necessario acquisire dati e informazioni “utili”. Oggi si sente spesso dire che ci si deve basare sull’evidenza. E i numeri sono per definizione portatori di “evidenza”. Evidenza e valori decisionali Ma cosa è l’evidenza? Vediamo un esempio. Negli anni dal 1998 al 2002 l’Istituto Nazionale di Statistica ha registrato moltissime varibili. Tra queste ne ho scelte due. Ho quindi ipotizzato che le due variabili siano legate da una relazione lineare, e utilizzando la regressione lineare ho ottenuto per la retta di equazione y = a + bx una intercetta a = 270,68011 e un coefficiente angolare b = 0.20503. Il coefficiente di correlazione r = 0,97489 è significativo, nel senso che indica che le due variabili variano congiuntamente: senza ombra di dubbio. Ma vediamo di che si tratta. La variabile x, in ascisse è: Procedimenti civili di primo grado pendenti a fine anno.Da “ISTAT, Annuario statistico italiano 2004, pag. 136. Tavola 6.1 - Movimento dei procedimenti civili per grado di giudizio e ufficio giudiziario – Anni 1998-2002”. La variabile y, in ordinate è: Casi [di AIDS] diagnosticati.Da “Notiziario dell’Istituto Superiore di Sanità, Supplemento 1-2007, Aggiornamento dei casi di AIDS notificati in Italia e delle nuove diagnosi di infezione da HIV, pag. 4. Tabella 1 - Distribuzione annuale dei casi di AIDS, dei casi corretti per ritardo di notifica, dei decessi e del tasso di letalità” Le fonti sono assolutamente documentate e assolutamente autorevoli. Ed esiste una “evidenza” suffragata dai numeri che le due variabili variano congiuntamente.
8. Teorema di Bayes e decisioni mediche
Tuttavia l’evidenza dei numeri è in contrasto con la ragionevolezza: perchè non abbiamo un modello che faccia un’ipotesi ragionevole su come all’aumentare dell’efficienza nell’amministrazione della giustizia civile la gente si ammali meno di AIDS. I due fatti sono “evidentemente” slegati, anche se dal punto di vista statistico “evidentemente” correlati (per la gioia di Mark Twain). Ora, dato che si tratta di una cosa “non evidente”, e anzi parrebbe “evidente” il contrario, lo dichiaro esplicitamente: il mio scopo non è di polemizzare con la statistica o con la medicina basata sull’evidenza (per discutere dei sottili legami che intercorrono tra quest’ultima, la statistica e l’approccio presentato in questo sito, rimando alla successiva parte su teorema di Bayes e medicina basata sull’evidenza). Voglio invece ricordare quanto sia delicato interpretare anche un dato numerico, poiché che la diagnostica di laboratorio proprio su questo si basa: vediamo come. Per analisi il cui risultato può essere espresso in una scala numerica continua, tradizionalmente, la decisione medica in merito allo stato di salute di un paziente (sano o malato?) presuppone di cambiare l’orientamento diagnostico in corrispondenza di valori soglia prefissati, i “valori decisionali”.
* definizione dell’Organizzazione Mondiale della Sanità Dal punto di vista delle strategie i criteri utilizzati per definire i vari tipi di valori decisionali sono semplici e logici:→ gli intervalli di riferimento rappresentano l’ambito di valori che include il 95% dei risultati osservati in un gruppo di controllo di soggetti sani. Sono quelli riportati nel referto di laboratorio. Come conseguenza della definizione, un soggetto sano che esegue una analisi di laboratorio ha il 95% di probabilità che il proprio valore risulti all’interno degli intervalli di riferimento, e un soggetto sano che esegue 20 analisi di laboratorio ha una probabilità di (0,95)20 = 0,358486 che tutti i risultati rientrino all’interno degli intervalli di riferimento. O, in altri termini, su 100 soggetti sani che eseguono ciascuno 20 analisi, solamente il 36% circa avrà tutti i valori all’interno degli intervalli di riferimento;→ gli intervalli terapeutici dei farmaci rappresentano l’ambito di valori che caratterizza l’efficacia terapeutica. Concentrazioni inferiori non garantiscono l’efficacia. Concentrazioni superiori indicano che la dose somministrata è eccessiva;→ i valori che definiscono la malattia forniscono, per l’appunto, la definizione della malattia. Un altro esempio oltre a quello dell’anemia: una glucosio a digiuno uguale o superiore a 126 mg/dL (milligrammi per decilitro di plasma) fornisce la diagnosi di diabete mellito. Da notare la differenza, oltre che numerica, concettuale rispetto agli intervalli di riferimento del glucosio, che vanno da 60 a 110 mg/dL;→ i valori desiderabili sono valori raccomandati in relazione a specifici obiettivi. Nel caso del colesterolo totale nel siero, essendo nota la correlazione tra aumento del colesterolo e aumento del rischio di malattia cardiovascolare, il valore di 200 mg/dL è stato scelto sulla base di un consenso internazionale in merito al fatto che il mantenimento di una concentrazione del colesterolo inferiore a tale limite consente di ridurre in modo significativo l’incidenza di malattie cardiovascolari;→ i valori di allarme sono valori che impongono un intervento. Nel caso di un potassio superiore a 6,7 mmol/L, quale si può riscontrare in caso di grave insufficienza renale, l’intervento si rende necessario a causa del rischio imminente di aritmie cardiache mortali;→ le differenze critiche rappresentano la minima differenza tra due risultati consecutivi che può essere ritenuta statisticamente significativa. Si supponga di sottoporre a trattamento dietetico un paziente con un colesterolo di 243 mg/dL, e che un successivo controllo a distanza fornisca un valore di 225 mg/dL. La terapia è stata efficace? Probabilmente no, in quanto per il colesterolo è noto che la differenza critica è del 12%, quindi il valore avrebbe dovuto scendere almeno a 214 mg/dL perché la differenza potesse essere attribuita al trattamento e non al caso. I valori decisionali fissi sono degli stereotipi: ovviamente utili, ma che tendono a forzare l’interpretazione del dato di laboratorio utilizzando un riferimento collettivo, e quindi a prescindere dal fatto che ogni individuo, e quindi ogni caso clinico, differisce sottilmente da tutti gli altri. Per capire come si sia resa sempre più evidente la necessità di introdurre nella decisione medica un criterio di flessibilità, che consenta di adattare il risultato della misura (oggettivo) al caso clinico specifico, unico e irripetibile, si consideri l’esempio degli enzimi (amminotransferasi o, secondo la vecchia nomenclatura, transaminasi) per la diagnosi dell’epatite. La situazione apparsa ai primi “esploratori” della biochimica dell’organismo umano può essere emblematicamente così descritta (risultati in U/L)
Questa prima tabella vuole evidenziare il fatto che un tempo erano poche le analisi eseguite, e pochi i controlli sani utilizzati come confronto. Inoltre i pazienti erano selezionati in base alla presenza di segni clinici importanti, per esempio, nel caso dell’epatite, in base alla presenza di ittero (un danno del fegato elevato al punto tale da determinare una diminuzione della capacità di eliminare la bilirubina nella bile). Il che implica una compromissione più consistente del fegato, quindi un aumento più elevato delle amminotransferasi. Nella distribuzione dei valori, esemplificati in questa prima tabella, appariva, ai primi “esploratori” della biochimica, una discontinuità “evidente”, a livello della quale era “intuitivo” porre il limite per distinguere tra sani e malati. Oggigiorno sono molte le analisi eseguite, molti i controlli sani di cui disponiamo, i pazienti solo raramente (tipicamente solo quando ricoverati in ospedale) sono selezionati in base alla presenza di segni clinici importanti, come la presenza di ittero. La spinta verso una diagnosi sempre più precoce comporta il fatto che oggigiorno la situazione delle transaminasi nei confronti della diagnosi di epatite può essere emblematicamente così descritta (risultati in U/L)
Data la sovrapposizione tra le distribuzioni dei valori nei sani e nei malati, il valore decisionale in questa seconda tabella risulta tutt’altro che evidente. Ecco allora la domanda: quale è il valore che consente di distinguere tra malati e sani? Ovvero, più in generale: esiste in assoluto un razionale da cui derivare un metodo/un algoritmo per stabilire il valore decisionale che distingue tra malati e sani? Il concetto di “mucchio di sabbia” è intuitivo. Il problema sorge quando, dal mucchio, incominciamo a togliere i granelli di sabbia uno ad uno [a]. Quando è che il mucchio di sabbia non è più tale, e diventa un “non-mucchio”? Analogamente, se prendiamo valori di transaminasi intuitivamente “non-normali”, e incominciamo a ridurli senza soluzioni di continuo, di una U/L per volta, quale è il valore che segna la transizione tra valori “non-normali” e valori “normali”? L’approccio bayesiano consente di formalizzare la presenza, tra il bianco e il nero, dei livelli di grigio. Se probabilità (p) di malattia = 0 significa “certamente sano”, e probabilità (p) di malattia = 1 significa “certamente malato”, ciò avviene raramente nella pratica medica. Prevalgono i casi di 0 < p < 1. Il confine tra salute e malattia è sfumato. L’approccio bayesiano, consentendo di definire il valore decisionale di volta in volta, in funzione di specifiche esigenze mediche, permette di formalizzare in modo scientificamente, metodologicamente e numericamente rigoroso quanto il “buon senso” medico aveva da tempo intuito [1]. Informazione e valori decisionali Tuttavia una cosa ce la dobbiamo domandare: perché il teorema di Bayes non è riuscito ad “automatizzare” il buon senso medico, quindi ad “automatizzare” la diagnosi medica? Innanzitutto la forma presentata per un test diagnostico e una malattia dal punto di vista computazionale è banale: ma bisogna ricordare che se teorema di Bayes è generalizzato a n ipotesi concomitanti (come nel caso di una diagnosi differenziale tra più malattie), nascono rapidamente seri problemi computazionali. Limitiamoci quindi al caso più semplice, quello di un test diagnostico e una malattia. La macchina matematica è perfetta, tanto che oggi il data mining bayesiano [b] rappresenta uno strumento sempre più utilizzato: e filtri bayesiani stanno alla base dell’efficienza nella ricerca dell’informazione che chiunque è in grado di sperimentare utilizzando un motore di ricerca come Google. Ma un sistema di supporto alle decisioni, quale è quello che pretendiamo di realizzare applicando ai nostri dati il teorema di Bayes, è influenzato da due diversi fattori: la qualità della macchina che ne costituisce il motore inferenziale, e la qualità dell’informazione in ingresso.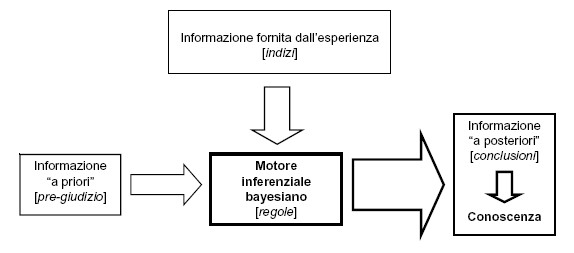 
Ecco quindi, una volta assunto che il motore inferenziale bayesiano è tecnicamente, logicamente e funzionalmente ineccepibile, che siamo ritornati al punto cruciale: l’informazione. PROBLEMA 10E’ stato messo a punto un nuovo test per la diagnosi prenatale, su liquido amniotico, di una malattia genetica, per la quale è nota una prevalenza di 3 su mille neonati. Il test ha una sensibilità del 100%. Per la specificità del test, che è pari al 99,5% (tecnicamente si dice che 99,5% è la “stima puntiforme” del valore di specificità), sono riportati in letteratura anche i limiti di confidenza al 95%, che rappresentano i limiti all’interno dei quali si colloca (con una probabilità del 95%) l’incertezza con cui è stata stimata la specificità: tali limiti vanno da 99,0% a 99,9%.Quale è il grado di incertezza che può essere attribuito al valore predittivo del test positivo? La risposta può essere ricavata dalla seguente tabella, nella quale il valore predittivo del test positivo è stato calcolato per i due valori di specificità (99,9 e 99,0%) che rappresentano i limiti superiore e inferiore dell’incertezza all’interno dei quali si colloca il valore di specificità del 99,5%.
Come si vede se, a fronte di una specificità (stimata) del 99,5%, la specificità “vera” fosse del 99,9% il valore predittivo del test positivo sarebbe del 75,1%, mentre se la specificità “vera” fosse del 99,0% il valore predittivo del test positivo sarebbe del 23,1%. Particolarmente interessante al nostro scopo il fatto che una misura che ha una incertezza originaria che va dal 99,0% al 99,9%, quindi di circa una parte su cento, porta a una conclusione (il valore predittivo del test positivo) con una incertezza che va dal 23,1% al 75,1%, che è oltre 50 volte l’incertezza iniziale! PROBLEMA 11E’ stato messo a punto un nuovo test per la diagnosi dell’artrite reumatoide. Il test viene provato in via preliminare una clinica universitaria, presso la quale la metà circa dei pazienti è affetta da artrite reumatoide Per questo motivo vi è la rara opportunità di provarlo su ben 500 pazienti affetti da artrite reumatoide e su 500 pazienti affetti da altre patologie reumatologiche diverse dall’artrite reumatoide. Il test dimostra di avere una sensibilità del 100% e una specificità del 95%. Il test viene immesso sul mercato includendo nel bugiardino i dati di sensibilità e di specificità, che sono in assoluto i migliori per un test per la diagnosi di artrite reumatoide. Dopo l’immissione in commercio, il test si diffonde rapidamente proprio per queste sue notevoli caratteristiche. Tuttavia l’utilizzo del test da parte dei medici di medicina generale dimostra risultati meno soddisfacenti di quanto atteso.Esiste un razionale che spieghi perché nella pratica il test risulta meno soddisfacente di quanto prevedibile in base ai dati ottenuti nella fase preliminare? La risposta può essere ricavata dalla seguente tabella, nella quale il valore predittivo del test positivo è stato calcolato per diversi valori di prevalenza della malattia.
Consideriamo il valore predittivo del test positivo. Nel corso delle prove presso la clinica universitaria, il test è stato applicato ad una casistica di 500 malati e di 500 sani: quindi con una prevalenza della malattia del 50%. In queste condizioni il valore predittivo del test positivo, quindi la probabilità di essere malato per un soggetto con un test positivo, era del 95,2%. Una volta entrato nell’uso, il test è stato poi applicato a casistiche ambulatoriali, non selezionate, con prevalenza della malattia di gran lunga inferiore. Dalla tabella appare evidente come l’applicazione del test in una condizione di prevalenza della malattia più “realistica”, con valori che vanno dal 10% all’1%, comporta un valore predittivo del test positivo che va dal 69% al 16,8%, o in altre parole comporta il fatto che su 100 soggetti con un test positivo, da 31 (per una prevalenza della malattia del 10%) a 83 (per una prevalenza della malattia dell1%) sono soggetti sani. Ecco perchè nella pratica il test risulta meno soddisfacente di quanto poteva sembrare in base ai dati preliminari. Le possibili conseguenze determinate dalla dipendenza del valore predittivo del test dalla prevalenza della malattia, sono ben descritte in Gerhardt e Keller [1], e comportano la necessità nel corso della messa a punto e della applicazione di un test diagnostico di valutarne con la massima cura tutti gli aspetti. Da questi due problemi possiamo trarre alcune considerazioni generali. Normalmente per i test di laboratorio sono note la sensibilità e la specificità. Entrambe sono state misurate, quindi sono caratterizzate da un certo grado di incertezza (anche se questo fatto viene sistematicamente ignorato). Coloro che pensano che gli errori tendano ad elidersi si devono ricredere: non solo l’incertezza delle premesse non può essere eliminata dalle conclusioni che da essa trarremo, ma una piccola incertezza (dell’informazione) in ingresso viene amplificata (propagazione dell’errore) e determina un incertezza (dell’informazione) in uscita addirittura maggiore. Per il calcolo del valore predittivo è necessaria anche la prevalenza della malattia. Anche questa misura è caratterizzata da un certo grado di incertezza. Ma esiste per la prevalenza un ulteriore complicazione. La prevalenza varia moltissimo sia nel tempo (basti pensare alla fluttuazione della prevalenza dell’influenza e del morbillo nel corso dell’anno), sia in relazione al contesto (la prevalenza di sieropositivi per l’HIV è diversa nei diversi continenti, in Italia è diversa tra la popolazione generale e le classi di soggetti con comportamenti a rischio, eccetera). La fluttuazione nel tempo e la sensibilità al contesto della prevalenza creano ovviamente una enorme difficoltà per molte malattie (paradossalmente questo è un problema minore per le malattie genetiche, come ad esempio la sindrome di Down, per la quale la prevalenza è stabile ed è nota anche in modo molto accurato per le varie classi di età cui appartiene la gravida). Combinando le incertezze iniziali di sensibilità, specificità e prevalenza, e le variazioni di prevalenza determinate dal contesto, arriviamo a conclusioni inevitabilmente incerte. Aggiungiamo che ogni caso clinico è unico. Quindi vorremmo cambiare in modo dinamico la soglia che discrimina tra sani e malati in relazione allo specifico caso clinico, e quindi allo specifico obiettivo clinico: per fare questo è necessario disporre delle distribuzioni dei risultati del test nei sani e nei malati (non esistono, se non negli studi clinici controllati, database contenenti sia i risultati delle analisi sia le diagnosi, e per di più non esiste un fromato standard per esprimere questo risultati, che quindi non possono essere integrati). Tutto questo rende per ora scarsamente praticabile affrontare in modo rigorosamente computazionale un approccio che non solo il laboratorio, ma anche i clinici hanno riconosciuto come connaturato con il “modo di pensare diagnostico” (per questo rimando nuovamente all’articolo di Gill, Sabin e Schmid comparso sul BMJ, e dal titolo “Why clincians are natural bayesians”. Espressione del teorema di Bayes in termini di odds e rapporto di verosimiglianza Da un punto di vista razionale la strategia che emerge dalle brevi considerazioni fatte sopra è abbastanza chiara, e si deve basare su alcuni punti “forti”:→ una informazione medica (diagnosi cliniche) assolutamente accurata e standardizzata;→ una informazione di laboratorio (risultati dei test di laboratorio) assolutamente accurata e standardizzata; → una completa standardizzazione e integrazione nella circolazione dell’informazione medica;→ accesso del clinico all’informazione (distribuzioni dei risultati dei test di laboratorio e diagnosi cliniche associate) che serve, nel momento in cui serve, nel posto in cui serve. Questo, detto per inciso, corrisponderà per la diagnostica di laboratorio ad un nuovo paradigma [2], caratterizzato da due linee di tendenza principali. La prima è che il referto di laboratorio non sarà più lo strumento cartaceo, rigido e limitato di oggi, ma un referto elettonico interattivo, in grado di generare in tempo reale l’informazione ricercata dal medico. La seconda, che è strettamente correlata con la prima, è che cambierà completamente il ruolo delle figure che operano in laboratorio. La cui attività si sposterà sempre più dal campo analitico al settore dell’informazione (medica di laboratorio). Il valore aggiunto che dovranno fornire nell’ambito della loro professione sarà rappresentato dalla capacità di produrre una informazione di laboratorio accurata e integrabile in tempo reale con il resto dell’informazione clinica, per garantire al medico l’informazione che serve, nel momento in cui serve e nel posto in cui serve. Valorizzando appieno il senso della diagnostica di laboratorio: estendere i sensi del medico (mediante l’informazione prodotta a livello morfologico, biochimico e molecolare). Per fissare questo concetti pensiamo all’esempio (qui necessariamente molto semplificato) di un medico alla prese con l’interpretazione i risultati di uno specifico test di laboratorio. Supponiamo di lavorare con la logica attuale (intervalli di riferimento fissi, al più separati per sesso e classi di età) e con un referto cartaceo. Supponiamo che l’intervallo di riferimento per il test sia identico per entambi i sessi e per tutte le età, e sia “inferiore a 33”. In altre parole il test è considerato negativo se il risultato è inferiore a 33, e considerato positivo se il risultato è uguale o superiore a 33. Il medico deve interpretare il risultato di due pazienti, uno con un valore di 35, un altro con un valore di 118. Entrambi i risultati sono confrontati con il valore soglia di 33. Per il medico è “evidente” e intuitivo, ai fini della diagnosi di una malattia, attribuire al valore di 118 un “peso” maggiore di quello attribuito al valore di 35. E’ “evidente” e intuitivo, ma non quantificabile. Supponiamo ora invece di lavorare con la logica bayesiana e con un referto elettronico interattivo. Come prima cosa il medico accede via web al referto elettronico interattivo del paziente e, visto il risultato, richiede le distribuzioni dei risultati dello specifico test nei soggetti non affetti (sani) e nei soggetti affetti da una specifica malattia, quella che sta sospettando. Con un semplice click del mouse visualizza sensibilità e specificità corrispondenti alle diverse soglie che è possibile impostare per differenziare i malati dai sani (per maggiori dettagli vedere l’esempio tratto da Ministat).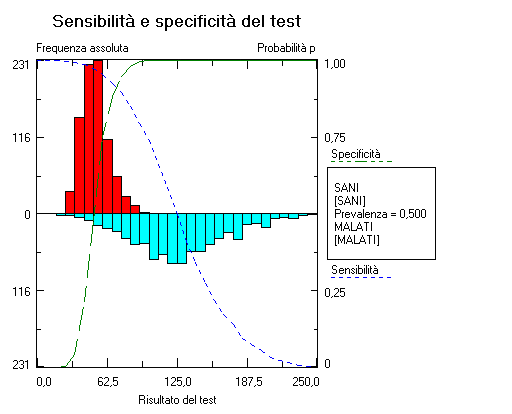 
Quindi il medico richiede la visualizzazione del valore predittivo del test positivo e del valore predittivo del test negativo corrispondenti. 
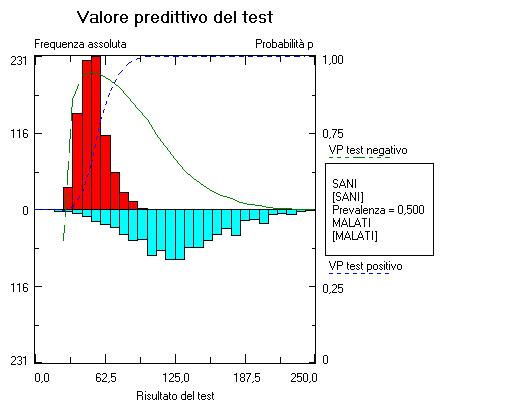Desiderando essere più analitico di quanto permesso dalla valutazione grafica, richiede infine una tabella che riassume numericamente i valori di sensibilità, specificità, valore predittivo dei test positivo e valore predittivo del test negativo che corrispondono all’utilizzo di valori soglia specifici al di sopra dei quali il test è cosiderato positivo (si tratta di una patologia che provoca un aumento della concentrazione dell’analita in questione).
Vediamo il caso del paziente con il risultato uguale a 35: ponendo la soglia di positività del test a un valore di 33 (lo stesso valore “fisso” del referto cartaceo) il medico ricava un valore predittivo del test positivo poco superiore a 0,50932 (diciamo poco superiore al 51%). Il risultato di 35 ha evidentemente un “peso” scarso ai fini della diagnosi, e non consente di confermare la malattia in questione. Vediamo il caso del paziente con il risultato uguale a 118: questa volta il medico decide di innalzare la soglia di positività del test a 117, ricavando un valore predittivo del test positivo pari a 1,0 (quindi uguale al 100%). Il risultato di 118 ha questa volta un “peso” molto maggiore, e consente di confermare la malattia in questione. Passare dagli intervalli di riferimento, fissi, ad una soglia che si può variare in modo dinamico, in relazione al singolo caso clinico, consente al medico di misurare in termini di probabilità la sempre maggiore verosimiglianza della diagnosi di malattia all’aumentare del valore del risultato del test: un concetto intuitivo nella mente di tutti, ma che solo l’approccio bayesiano consente di rendere in modo quantitativo! Se la visione del referto elettronico interattivo è ben lontana dal potere essere praticabile, niente paura. In attesa di sistemi di supporto alla diagnosi ancora al di là da venire, esiste comunque un approccio percorribile, basato su un compromesso epocale: coniugare il rigore computazionale del teorema di Bayes con la tendenza a soluzioni approssimative ma rapide (che ci deriva dall’imprinting risalente al Pleistocene della razionalità umana), prendendo semplicemente atto del fatto che l’informazione in ingresso è lontana dalla accuratezza desiderabile e che non ci sono metodi formali e pratici per raccoglierla in modo esaustivo. Questo approccio utilizza la terza formulazione del teorema di Bayes che vi presento, quella basata su odds e rapporto di verosimiglianza. Se, dopo avere letto questa parte, scaricate e aprite con Excel© o con Openoffice.org© Calc il file “Bayes_LR_p.xls”, vi potete anche esercitare. Questo approccio, che prevede in ingresso i valori di probabilità, ha una doppia valenza, sia didattica sia pratica, in quanto consente da un lato di familiarizzare con gli aspetti computazionali del teorema, e dall’altro di effettuare simulazioni (per esempio facendo variare la prevalenza) a partire dai dati di sensibilità e di specificità dei test che si ottengono dalla letteratura o dichiarati nella documentazione dei test diagnostici (come vedete i rapporti di verosimiglianza LR+ e LR- sono calcolati automaticamente). Nel file “Bayes_LR_num.xls” trovate invece l’approccio che corrisponde al percorso seguito quanto si raccolgono i risultati di un nuovo test di laboratorio in una casistica di soggetti affetti o non affetti da una specifica malattia, contando i casi da assegnare a ciascuna delle quattro caselle sopra individuate (numero di sani e numero di malati con test positivo e con test negativo) per determinare appunto le caratteristiche di sensibilità e di specificità del test in questione. Come vedete nel file la possibilità di disporre del numero di casi consente di calcolare per ciascuna di queste grandezze l’intervallo di confidenza (generalmente al 95%, ponendo z = 1,96, ma potete calcolarlo anche al 90% o al 99%, ponendo z rispettivamente uguale a 1,645 e 2,576). Si tratta di un punto cruciale, in quanto sia dal punto di vista epistemologico sia dal punto di vista metodologico è un “dovere scientifico” comunicare sempre il grado di incertezza che caratterizza l’informazione ottenuta. Pertanto la regola fondamentale è che qualsiasi conclusione statistica deve essere sempre accompagnata della misura dell’incertezza che la caratterizza, espressa sotto forma di intervallo di confidenza (vedere ad esempio in http://en.wikipedia.org/wiki/Confidence_interval). Al di là degli aspetti di tipo tecnico che caratterizzano i diversi modi di esprimere il teorema di Bayes che abbiamo visto (in termini di probabilità o in termini di numero di casi osservati, e per entrambi nella forma classica o in quella basata su odds e rapporto di verosimiglianza), resta tra la formulazione classica del teorema di Bayes e la formulazione basata sugli odds una differenza nell’interpretazione dell’informazione a priori (prima di avere eseguito il test) che è una differenza strutturale all’attuale epistemologia [3] e al mondo della statistica [c] e [4], come riconosciuto anche da Bland e Altman [5]. Per chiarire meglio cosa si intenda con ciò riprendiamo nuovamente l’esempio dovuto a De Finetti e che illustra la differenza che intercorre tra le tre principali definizioni di probabilità. Immaginiamo una partita di calcio per la quale gli eventi possibili sono:→ la vittoria della squadra di casa;→ la vittoria della squadra ospite;→ il pareggio.Sono tre i modi possibili per interpretare questi eventi:→ secondo la teoria (della probabilità) classica esiste 1 probabilità su 3 che avvenga la vittoria della squadra di casa;→ secondo la teoria (della probabilità) frequentista ci si può dotare di un almanacco, controllare tutte le partite precedenti e calcolare la frequenza di un evento;→ secondo la teoria (della probabilità) soggettiva, ci si può documentare sulla composizione della squadra, sullo stato di forma dei calciatori, sul terreno di gioco, e così via fino ad emettere un giudizio di probabilità (soggettiva). E’ possibile trasferire questi modelli alla diagnostica di laboratorio/diagnostica medica? Vediamo di nuovo i tre casi:→ la teoria (della probabilità) classica non è ovviamente applicabile né alla diagnostica di laboratorio né alla diagnostica medica: malattia e salute non sono stati (ovvero situazioni) equiprobabili;→ la formulazione classica del teorema di Bayes ci collega alla teoria (della probabilità) frequentista. Infatti in questo caso la probabilità a priori viene interpretata come la frequenza a priori della malattia (prevalenza della malattia). Questa è una probabilità “oggettiva” nella misura in cui viene considerata oggettiva la frequenza (della malattia);→ la formulazione del teorema di Bayes basata sul rapporto di verosimiglianza [6] ci collega alla interpretazione soggettiva della probabilità alla De Finetti. Utilizzando l’approccio basato sul rapporto di verosimiglianza e il nomogramma di Fagan si vede come, dato un LR+ (o un LR-) fisso, la probabilità pre-test è un concetto che va al di là della prevalenza, e diventa/può diventare, nelle mani di ciascun medico, un giudizio a priori che include le informazioni sullo stato precedente del paziente (anamnesi, malattie pregresse, conoscenza “storica” del paziente da parte dello stesso medico), quelle derivanti dall’esame clinico, da altri esami strumentali. Il tutto diventa un giudizio di probabilità soggettiva da parte del medico, una probabilità a priori (pre-test) che viene quindi corretta dal rapporto di verosimiglianza per dare la probabilità a posteriori (post-test). Il risultato del test diagnostico “inietta” informazione nel motore inferenziale, e fornisce valore aggiunto aumentando l’informazione (diagnostica) a disposizione del medico. Dato uno specifico test e il suo specifico valore di LR, la probabilità soggettiva a priori di ciascun medico diventa l’elemento che pilota la diagnosi verso la direzione giusta (o verso quella sbagliata), da un lato lasciando lo spazio alla osservazione quotidiana della differente “bravura” di ciascun medico, dall’altro lato indicando come questa componente “intuitiva” e di “soggettività”, che spiega la differente bravura, rappresenti ancora l’ostacolo alla formalizzazione rigorosa del processo di diagnosi medica. Ho riassunto gli argomenti trattati in questa parte anche in una presentazione, dal titolo teorema di Bayes e decisioni mediche. Ma per completare questa parte relativa alle decisioni mediche rimando alla successiva serie di considerazioni dal titolo teorema di Bayes e medicina basata sull’evidenza,che intendono sottolineare il fondamentale e per certi versi imprevisto collegamento teorico (epistemologico) e pratico che esiste tra teorema di Bayes e medicina basata sull’evidenza (EBM, Evidence Based Medicine). ********************************
Ecco quindi, una volta assunto che il motore inferenziale bayesiano è tecnicamente, logicamente e funzionalmente ineccepibile, che siamo ritornati al punto cruciale: l’informazione. PROBLEMA 10E’ stato messo a punto un nuovo test per la diagnosi prenatale, su liquido amniotico, di una malattia genetica, per la quale è nota una prevalenza di 3 su mille neonati. Il test ha una sensibilità del 100%. Per la specificità del test, che è pari al 99,5% (tecnicamente si dice che 99,5% è la “stima puntiforme” del valore di specificità), sono riportati in letteratura anche i limiti di confidenza al 95%, che rappresentano i limiti all’interno dei quali si colloca (con una probabilità del 95%) l’incertezza con cui è stata stimata la specificità: tali limiti vanno da 99,0% a 99,9%.Quale è il grado di incertezza che può essere attribuito al valore predittivo del test positivo? La risposta può essere ricavata dalla seguente tabella, nella quale il valore predittivo del test positivo è stato calcolato per i due valori di specificità (99,9 e 99,0%) che rappresentano i limiti superiore e inferiore dell’incertezza all’interno dei quali si colloca il valore di specificità del 99,5%.
Quindi il medico richiede la visualizzazione del valore predittivo del test positivo e del valore predittivo del test negativo corrispondenti. Desiderando essere più analitico di quanto permesso dalla valutazione grafica, richiede infine una tabella che riassume numericamente i valori di sensibilità, specificità, valore predittivo dei test positivo e valore predittivo del test negativo che corrispondono all’utilizzo di valori soglia specifici al di sopra dei quali il test è cosiderato positivo (si tratta di una patologia che provoca un aumento della concentrazione dell’analita in questione).
|
|
|
|
|
|
||
|
||
|
|
|
|
Ultimo aggiornamento: 20 febbraio 2023
NOTA SUI COLLEGAMENTIALLE FONTI BIBLIOGRAFICHE La maggior parte dei collegamenti ad articoli scientifici riportati nel sito fa riferimento a riviste online che forniscono gratuitamente l’articolo originale. In alcuni casi è necessario registrarsi sul sito per avere libero accesso agli articoli: questo accade per esempio con il BMJ. Quando i collegamenti fanno riferimento a fonti bibliografiche a pagamento, chi non ha sottoscritto un abbonamento con la rivista potrebbe vedere comparire un messaggio del tipo “access forbidden”, ma il più delle volte vedrà comparire una pagina che consente di acquistare online l’articolo originale.
scelti per voi
Programma di statistica Ministat (versione per Windows)
Programma di statistica Open Source R(per Linux, Mac OS X e Windows)
Manuale Merck di diagnosie terapia
L’articolo da non perdere...
Errori congeniti del metabolismo
I migliori libri del mese Leonard Mlodinow La passeggiata dell’ubriaco. Le leggi scientifiche del caso.Rizzoli Editore, 2009, pp. 294ISBN: 17034081
OpenOffice, la suite Open Source (per Linux, Mac OS X e Windows)
ebooks... Mauss, Berg, Rockstroh, Sarrazin, Wedemeyer.Hepatology - A clinical textbook. 10th Edition - 2020
Le lettureconsigliate
Atlante di anatomia del Bock
Tavole metaboliche
Informazioni: info@bayes.itScrivimi: webmaster@bayes.it
NOTA LEGALE L’interpretazione dei risultati delle analisi di laboratorio deve essere effettuata esclusivamente dal medico e alla luce dei dati clinici.Questo sito ha uno scopo esclusivamente educativo e formativo. Pertanto le informazioni in esso contenute possono essere utilizzate esclusivamente a scopo didattico, e anche in questo caso sotto la responsabilità personale di chi le utilizza, sia per sé stesso sia per terzi.Le informazioni contenute in questo sito non possono e non devono essere utilizzate né a scopo diagnostico, né a scopo prognostico, né a scopo terapeutico, né per qualsiasi attività che abbia un impatto sia diretto sia indiretto sullo stato di salute di un individuo o di più individui.Nessuna responsabilità può essere imputata all’autore per danni diretti o indiretti e di qualsivoglia natura che potrebbero essere causati a sé stessi o a terzi a causa di errori, imprecisioni, omissioni, interpretazioni o utilizzo dei contenuti di questo sito o dei siti cui esso fa riferimento.
E ora che i test genetici sono alla portata di tutti?Con meno di mille euro è possibile comprare un test genetico su Internet: si manda un piccolo campione di cellule e poi si aspetta la risposta. Ma... a che cosa serve la risposta? Un dossier di Marika De Acetis dall’Archivio storico del sito www.torinoscienza.it
[Home] [Errori cognitivi] [Epistemologia] [Teorema di Bayes] [Decisioni mediche] [Le basi biochimiche][Analisi tradizionali] [Analisi genetiche] [Qualità in laboratorio] [Statistica e laboratorio][Storia delle medicina] [Download] [Link] [Bacheca] [FAQ] [Chi sono]
Attualità in tema di eGFR:
I migliori libri del mese Giovanni Federspil Logica clinica. I principi del metodo in medicina.McGraw-Hill, 2004, pp. 368ISBN: 88 386 2984-6
Atlante di virologia
Dal settembre 2008oltre 400 000 visitatori
ebooks... M. BesozziErrori cognitivi, probabilità e decisioni mediche. Fate click sul titolo o scaricate il testo su tablet o smartphone con il codice a barre riportato qui sotto. 
Atlante dei protozoi intestinali
Atlante di citologia e istologia
Statistica e grafica con R
Espressione dei risultati nel laboratorio di chimica clinica
Pathology outlines
Atlante di anatomia del Gray
Atlante di ematologia
Atlante di parassitologia
Micobatteriologia clinica
Concetti, metodi e strumenti per una
buona informazione
ebooks... M. BesozziStatistica e grafica con R Fate click sul titolo o scaricate il testo su tablet o smartphone con il codice a barre riportato qui sotto. 
I migliori libri del mese Luigi Tesio I bravi e i buoni.Perché la medicina clinica può essere una scienza.Il Pensiero Scientifico Editore, 2015, pp. 216 ISBN: 978-88-490-0538-7
Gli inganni della correlazione:
Storia delle unità di misura
Questo sito è stato archiviato ed è reso disponibile esclusivamente come memoria storica: pertanto è escluso ogni suo possibile utilizzo medico. Le parti del sito riservate al teorema di Bayes rimangono concettualmente valide, ma declino qualsiasi responsabilità per la lenta ma inevitabile obsolescenza dei restanti contenuti dovuta alla comparsa di nuove analisi di laboratorio, di progressi nelle analisi genetiche, di link interrotti, e quant’altro.
.