6. Teorema di Bayes e informazione diagnostica
“L’errore nasce sempre dalla tendenza dell’uomo a dedurre la causa dalla conseguenza.”(Arthur Schopenhauer) “...questi problemi sono classificati come probabilità delle cause e sono i più importanti di tutti per le loro applicazioni scientifiche ... Un effetto potrebbe essere prodotto dalla causa a o dalla causa b. L'effetto è appena stato osservato. Ci domandiamo la probabilità che sia dovuto alla causa a. Questa è una probabilità di causa a posteriori. Ma non la potrei calcolare, se una convenzione più o meno giustificata non mi dicesse in anticipo quale è la probabilità a priori che la causa a entri in gioco.”(Henri Poincaré) Consideriamo un test di laboratorio per una patologia che comporta un innalzamento della concentrazione di uno specifico analita, e vediamo le tre situazioni paradigmatiche possibili.
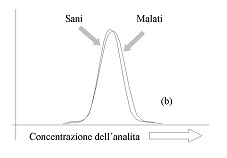
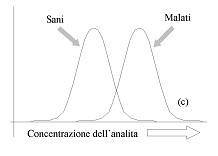
Il test ideale dovrebbe consentire di discriminare completamente tra sani e malati, come nell’esempio della figura (a). In un caso del genere, una volta eseguito il test, in base al suo risultato possiamo attribuire il paziente al gruppo dei sani o al gruppo dei malti con assoluta certezza. La situazione diametralmente opposta è quella indicata nella figura (b). In questo caso i risultati del test nel gruppo dei sani e nel gruppo dei malati sono identici: una volta eseguito il test, in base al suo risultato non sappiamo se attribuire il paziente al gruppo dei sani o al gruppo dei malati. Il test non può essere utilizzato per la diagnosi della malattia in questione. Si tratta di un test inutile. Nel caso di un test reale ci troviamo quasi sempre nella situazione indicata nella figura (c). La distribuzione dei risultati del test nei soggetti sani e nei soggetti malati è parzialmente sovrapposta, determinando così un certo grado di incertezza nella classificazione. Un test reale ci pone di fronte al paradosso del sorite, attribuito a Zenone: quale è il granello che fa passare un mucchio di sabbia in un non-mucchio? La cui forma moderna è: quale è il risultato di una specifica analisi di laboratorio che fa passare il soggetto dallo stato di “malato” a quello di “sano” (o viceversa)? Si tratta ovviamente di una bella domanda: alla quale troveremo il modo di rispondere utilizzando dei criteri di scelta quantitativi, misurabili, oggettivi.
E per fare questo come prima cosa dobbiamo costruirci un modello che rappresenti le grandezze in gioco come il seguente 
nel quale M+ indica la presenza della malattia, M- l’assenza della malattia, T+ un risultato positivo del test e T- un risultato negativo del test. In questo modo possiamo introdurre due delle tre grandezze in ingresso nel teorema: la sensibilità [del test di laboratorio], la specificità [del test di laboratorio]. La terza, la prevalenza [della malattia], è rappresentata semplicemente dal numero di malati nella popolazione (malati della specifica malattia nel momento in cui si utilizza il test). Vi presento poi una formulazione del teorema di Bayes che è particolarmente utile nella diagnostica di laboratorio. Mediante questa possiamo calcolare la grandezza in uscita dal teorema di Bayes: il valore predittivo di un test (di laboratorio). Se la domanda che ci poniamo è “quale è la probabilità che il paziente sia malato, avendo un test positivo?” possiamo calcolare il valore predittivo di un test positivo come 
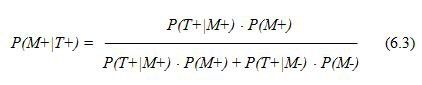mentre se la domanda che ci poniamo è “quale è la probabilità che il paziente sia sano, avendo un test negativo?” possiamo calcolare il valore predittivo di un test negativo come 
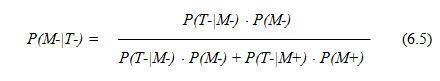Lo schema induzione/deduzione che abbiamo già visto si applica ovviamente anche a questa situazione.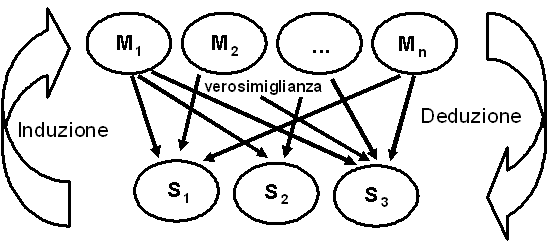 
nel quale M+ indica la presenza della malattia, M- l’assenza della malattia, T+ un risultato positivo del test e T- un risultato negativo del test. In questo modo possiamo introdurre due delle tre grandezze in ingresso nel teorema: la sensibilità [del test di laboratorio], la specificità [del test di laboratorio]. La terza, la prevalenza [della malattia], è rappresentata semplicemente dal numero di malati nella popolazione (malati della specifica malattia nel momento in cui si utilizza il test). Vi presento poi una formulazione del teorema di Bayes che è particolarmente utile nella diagnostica di laboratorio. Mediante questa possiamo calcolare la grandezza in uscita dal teorema di Bayes: il valore predittivo di un test (di laboratorio). Se la domanda che ci poniamo è “quale è la probabilità che il paziente sia malato, avendo un test positivo?” possiamo calcolare il valore predittivo di un test positivo come 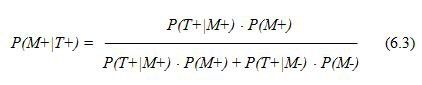mentre se la domanda che ci poniamo è “quale è la probabilità che il paziente sia sano, avendo un test negativo?” possiamo calcolare il valore predittivo di un test negativo come 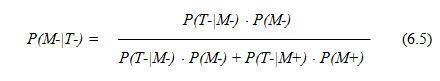Lo schema induzione/deduzione che abbiamo già visto si applica ovviamente anche a questa situazione. Conoscendo le cause (le malattie M1, M2. .... Mn), possiamo da queste dedurre gli effetti corrispondenti: è quanto viene fatto con lo studio della patologia medica. La soluzione del problema inverso, ovvero l’induzione, viene insegnata con la clinica medica, che insegna come affrontare una logica ribaltata, davanti al problema cardine che si incontra nella pratica medica quotidiana: un malato con una serie di sintomi e/o segni (S1, S2, S3), a partire dai quali dobbiamo risalire alla malattia. L’induzione è oltremodo più difficile, in quanto ad un sintomo e/o segno possono corrispondere più cause in termini di malattia. Il teorema di Bayes consente, a partire dai sintomi/segni osservati, di calcolare la verosimiglianza delle cause/malattie, espressa nell’unico modo possibile: in termini di probabilità. A questo punto, prima di procedere oltre, dovete avere la pazienza prima di familiarizzare con la formulazione del teorema di Bayes che vi ho presentato, quindi di familiarizzare ulteriormente con il teorema utilizzando i tre esempi sotto forma di problemi che vi ho fornito. Espressione classica del teorema di Bayes termini di probabilità P Per fare questo riprendiamo il problema 9. Un marcatore tumorale ha le seguenti caratteristiche: (i) è positivo in 95 su 100 pazienti con il cancro; (ii) è negativo in 95 su 100 pazienti senza in cancro; (iii) in media, 5 persone su una popolazione di 1000 hanno un cancro non ancora diagnosticato del tipo che il marcatore tumorale in questione rileva.Se il test è prescritto a un paziente selezionato casualmente in questa popolazione e l’esito è positivo, quale è la probabilità che il paziente abbia realmente il cancro?Analizziamo innanzitutto le tre affermazioni:→ “(i) è positivo in 95 su 100 pazienti con il cancro”, significa che il test ha un sensibilità del 95%, cioè che P=0,95;→ “(ii) è negativo in 95 su 100 pazienti senza in cancro”, significa che il test ha una specificità del 95%, cioè che P=0,95;→ “(iii) in media, 5 persone su una popolazione di 1000 hanno un cancro non ancora diagnosticato del tipo che il marcatore tumorale in questione rileva”, significa che la prevalenza della malattia rilevata dal test è del 5 per mille, cioè che P=0,005. Uno strumento per effettuare con semplicità i calcoli necessari Scaricate e aprite con Excel© o con OpenOffice.org© Calc il file “Bayes_p.xls”. Nella cella A2 inserite il valore P della sensibilità (0.95), nella cella B2 inserite il valore P della specificità (0.95), e nella cella C2 inserite il valore P della prevalenza (0.005). Poichè nella cella D2 ho inserito il teorema di Bayes con la formula per il calcolo del valore predittivo di un test positivo =(C2*A2)/((C2*A2)+((1-C2)*(1-B2))) e nella cella E2 ho inserito il teorema di Bayes con la formula per il calcolo del valore predittivo di un test negativo =(B2*(1-C2))/((B2*(1-C2))+((1-A2)*C2)) vedrete calcolati automaticamente tali valori. Che più precisamente sono: il valore predittivo del test positivo uguale a 0,087 (8,7%), e il valore predittivo del test negativo uguale a 1,000 (100%: in realtà questo 100% è un effetto dell’arrotondamento a tre decimali: se portate a quattro il numero dei decimali, otterrete 0,9997 cioè 99,97%). Questo approccio, che prevede in ingresso i valori di probabilità, ha una doppia valenza, sia didattica sia pratica, in quanto consente da un lato di familiarizzare con gli aspetti computazionali del teorema, e dall’altro di effettuare simulazioni (per esempio facendo variare la prevalenza) a partire dai dati di sensibilità e di specificità dei test che si ottengono dalla letteratura o dichiarati nella documentazione dei test diagnostici. L’approccio alternativo, basato sulla disponibilità del numero dei casi (numero di sani e numero di malati con test positivo e con test negativo) è riportato nella parte su teorema di Bayes e strategie diagnostiche e risulterà, come vedremo, fondamentale per ricavare l’intervallo di confidenza delle grandezze calcolate, altro elemento cruciale per giudicare la qualità dell’informazione fornita dal test. Interpretazione dei risultati Il valore predittivo di un test positivo è, per definizione, la probabilità di essere malato per un soggetto con un test positivo. Prendiamo 100 soggetti con un test positivo per il marcatore tumorale: in base ai risultati ottenuti (arrotondando 8,7 a 9) 9 di essi saranno malati, mentre i rimanenti 91 saranno sani. In altre parole questo significa che su 100 persone con un test positivo per il marcatore tumorale vi saranno 9 veri positivi (i malati classificati come tali dal test) e 91 falsi positivi (i sani classificati come malati dal test). Il valore predittivo di un test negativo è, per definizione, la probabilità di essere sano per un soggetto con un test negativo. Prendiamo 100 soggetti con un test negativo per il marcatore tumorale: in base ai risultati ottenuti (e mantenendo l’arrotondamento di 99,97 a 100) 100 di essi saranno sani, mentre nessuno sarà malato. In altre parole questo significa che su 100 persone con un test negativo per il marcatore tumorale:vi saranno 100 veri negativi (i sani classificati come tali dal test) e non vi saranno falsi negativi (i malati classificati come sani dal test). La prevalenza della malattia è la probabilità a priori, cioè la probabilità di essere affetto da un cancro del tipo che il marcatore tumorale in questione rileva prima di eseguire il test: è uguale al 5 per mille (P = 0,005). Il valore predittivo del test positivo è la probabilità a posteriori, dopo avere eseguito il test: ed è uguale all’8,7% (P = 0,087). La differenza tra le due P = 0,082 è il valore aggiunto in termini di informazione che il test fornisce alla diagnosi.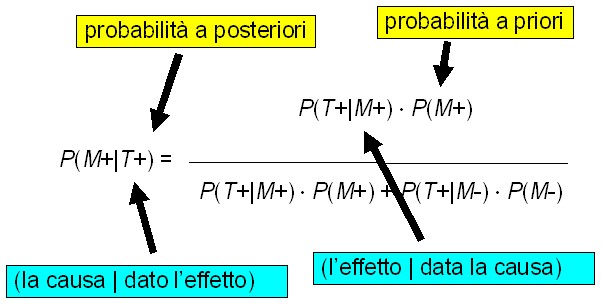 
L’esempio riportato, che si riferisce ad un ottimo test diagnostico (sensibilità e specificità entrambe pari al 95%), è paradigmatico. Lo scarso valore aggiunto, in termini di informazione, che i marcatori tumorali forniscono alla diagnosi, rappresenta il razionale per cui se ne sconsiglia l’uso come test di screening in una popolazione non selezionata. Il teorema di Bayes rappresenta l'unico strumento che consente di fornire una misura quantitativa, e quindi oggettiva, espressa in termini di informazione, del valore aggiunto fornito da un test diagnostico. Dal punto di vista epistemologico risultano evidenti nel teorema di Bayes:→ la capacità di formalizzare il meccanismo con cui si ribaltare la logica, da l’effetto|data la causa a la causa|dato l’effetto, passando dalla deduzione all’induzione (che risulta per definizione solo probabile);→ la capacità di formalizzare il meccanismo con cui l’informazione fornita dall’esperienza (lo specifico risultato del test di laboratorio) si somma all’informazione a priori, aumentando la nostra conoscenza;→ la capacità di misurare l’informazione che un test diagnostico fonisce alla diagnosi medica [a]. Dal punto di vista pratico risulta evidente dal teorema di Bayes che:→ in condizioni di bassa prevalenza diminuisce il valore predittivo del test positivo;→ in condizioni di bassa specificità del test diminuisce il valore predittivo del test positivo;→ in condizioni di bassa specificità e di bassa prevalenza aumenta il valore predittivo del test negativo, quindi un test diventa utile soprattutto per escludere la malattia. Questi argomenti sono ulteriormente trattati nelle prossime parti. In particolare per quanto riguarda la capacità del teorema di Bayes di formalizzare il meccanismo con cui l’informazione fornita dall’esperienza (lo specifico risultato del test di laboratorio) si somma all’informazione a priori, aumentando la nostra conoscenza, vedremo come, in alternativa all’interpretazione frequentista qui illustrata, nella quale la probabilità a priori è rappresentata dalla prevalenza della malattia, sia possibile adottare un approccio “soggettivista”, forse per alcuni aspetti più vicino al modo di ragionare del clinico. Inoltre verranno approfondite ulteriormente le conseguenze della bassa specificità di un test di laboratorio e della bassa prevalenza della malattia. Per le definizioni di base rimando anche alle Statistics Notes di Altman nella pagina iniziale del teorema di Bayes. Ho riassunto gli argomenti trattati in questa parte in una presentazione, dal titolo teorema di Bayes e informazione diagnostica. Informazione diagnostica e curve ROC ROC è l'acronimo di Receiver Operating Characteristic (caratteristiche operative del ricevitore) e ha un’origine che vale la pena di ricordare. Perchè il ricevitore in questione è il radar. Durante la seconda guerra mondiale il problema era, nell'ambito del rumore di fondo presente nei segnali radar, riconoscere il segnale causato dalla presenza di oggetti nemici sui campi di battaglia (tipicamente nei cieli, ma anche in mare). Si tratta di un classico problema di rapporto segnale/rumore [b] che è stato affrontato dagli ingegneri nell'ambito della teoria della rilevazione del segnale. Vediamo un primo esempio numerico, rappresentato dalla seguente serie di dati: 3, 4, 6, 2, 6, 5, 4, 5, 3, 3, 6, 12, 4, 5, 6, 6, 7, 4, 5, 4, 4, 4, 3, 5, 11, 3, 3, 5, 2, 5, 4, 3, 2 Supponiamo di avere un filtro digitale (in realtà negli anni '40 del secolo scorso si avevano a disposizione dati analogici e filtri analogici, ma concettualmente la situazione è identica), un filtro che possa essere variato in continuo, ponendo la prima volta la soglia a 12, e considerando "rumore" i valori inferiori a 12 e "segnale" i valori uguali o superiori a 12, ponendo la seconda volta la soglia a 11, e considerando "rumore" i valori inferiori a 11 e "segnale" i valori uguali o superiori a 11, e così via. Dopo avere filtrato il segnale utilizzando tutte le possibili soglie (gli interi compresi tra 12 e 2) otteniamo la seguente serie di dati (il rumore viene posto convenzionalmente uguale a “_”): _, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, 7, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, 6, _, 6, _, _, _, _, _, 6, 12, _, _, 6, 6, 7, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, 6, _, 6, 5, _, 5, _, _, 6, 12, _, 5, 6, 6, 7, _, 5, _, _, _, _, 5, 11, _, _, 5, _, 5, _, _, __, 4, 6, _, 6, 5, 4, 5, _, _, 6, 12, 4, 5, 6, 6, 7, 4, 5, 4, 4, 4, _, 5, 11, _, _, 5, _, 5, 4, _, _3, 4, 6, _, 6, 5, 4, 5, 3, 3, 6, 12, 4, 5, 6, 6, 7, 4, 5, 4, 4, 4, 3, 5, 11, 3, 3, 5, _, 5, 4, 3, _3, 4, 6, 2, 6, 5, 4, 5, 3, 3, 6, 12, 4, 5, 6, 6, 7, 4, 5, 4, 4, 4, 3, 5, 11, 3, 3, 5, 2, 5, 4, 3, 2 Supponendo che i segnali di intensità 11 e 12 provengano dagli oggetti che volevamo rilevare (quindi, nell'esempio aeronautico, da due aerei), abbiamo individuato ciò che ci interessava in mezzo al rumore di fondo del radar (valori da 7 in giù). In questo esempio, come avete notato, mancano completamente i valori 8, 9 e 10. Il “rapporto segnale/rumore” (11 o 12 di segnale, contro 7 o meno di rumore) è elevato: e questo rende “evidente” la soglia tra rumore e segnale (il legame che intercorre tra valore soglia prescelto, che qui potrebbe essere 8, 9, 10 o 11, e sensibilità e specificità, è discusso nella parte su Teorema di Bayes e strategie diagnostiche). Ma la realtà è sempre fastidiosamente ambigua, e nella pratica si ha a che fare con distribuzioni dei valori che assomigliano di più a quella riportata in questo secondo esempio: 3, 4, 6, 2, 6, 9, 5, 4,10, 8, 10, 8, 5, 9, 6, 12, 11, 4, 7, 6, 8, 9, 3, 3, 5, 9, 12, 10, 4, 6, 7, 8, 6, 5, 4 Dopo avere filtrato il segnale utilizzando tutte le possibili soglie (interi compresi tra 12 e 2) otteniamo ora la seguente serie di dati: _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, _, _, _, _, 12, 11, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, 10, _, 10, _, _, _, _, 12, 11, _, _, _, _, _, _, _, _, _, 12, 10, _, _, _, _, _, _, __, _, _, _, _, 9, _, _, 10, _, 10, _, _, 9, _, 12, 11, _, _, _, _, 9, _, _, _, 9, 12, 10, _, _, _, _, _, _, __, _, _, _, _, 9, _, _, 10, 8, 10, 8, _, 9, _, 12, 11, _, _, _, 8, 9, _, _, _, 9, 12, 10, _, _, _, 8, _, _, __, _, _, _, _, 9, _, _, 10, 8, 10, 8, _, 9, _, 12, 11, _, 7, _, 8, 9, _, _, _, 9, 12, 10, _, _, 7, 8, _, _, __, _, 6, _, 6, 9, _, _, 10, 8, 10, 8, _, 9, 6, 12, 11, _, 7, 6, 8, 9, _, _, _, 9, 12, 10, _, 6, 7, 8, 6, _, __, _, 6, _, 6, 9, 5, _, 10, 8, 10, 8, 5, 9, 6, 12, 11, _, 7, 6, 8, 9, _, _, 5, 9, 12, 10, _, 6, 7, 8, 6, 5, __, 4, 6, _, 6, 9, 5, 4, 10, 8, 10, 8, 5, 9, 6, 12, 11, 4, 7, 6, 8, 9, _, _, 5, 9, 12, 10, 4, 6, 7, 8, 6, 5, 43, 4, 6, _, 6, 9, 5, 4, 10, 8, 10, 8, 5, 9, 6, 12, 11, 4, 7, 6, 8, 9, 3, 3, 5, 9, 12, 10, 4, 6, 7, 8, 6, 5, 43, 4, 6, 2, 6, 9, 5, 4, 10, 8, 10, 8, 5, 9, 6, 12, 11, 4, 7, 6, 8, 9, 3, 3, 5, 9, 12, 10, 4, 6, 7, 8, 6, 5, 4 Il problema è che questa volta i valori variano da 2 a 12 senza soluzioni di continuo: e la soglia tra segnale e rumore non è più “evidente” come sembrava esserlo nel primo caso. Ci troviamo di fronte a una della infinite varianti del paradosso del sorite di Zenone: quale è il granello che fa passare un mucchio di sabbia in un non-mucchio? La cui forma in questo caso è: quale è il valore che segna la transizione da un segnale a un non-segnale, ovvero quale è il valore soglia al di sotto del quale dobbiamo pensare che non si tratti più di un segnale (un aereo), ma si tratti semplicemente di rumore di fondo? Questo secondo esempio illustra una situazione in cui il rapporto segnale/rumore è ridotto, e quindi abbiamo difficoltà a distiguere l'uno dall'altro. Gli ingegneri hanno modellizzato il problema trovando una generalizzazione che consente di affrontarlo "more scientifico". E come vedete anche nella Wikipedia [1] si tratta del modello utilizzato per la diagnostica di laboratorio e la diagnosi medica in generale. Nelle quali il risultato del test nei malati è il segnale, il risultato del test nei sani è il rumore (di fondo). E la curva ROC è costruita semplicemente riportando in ascisse la sensibilità e in ordinate (1 - specificità), come si può vedere nella figura seguente che è tratta dell’esempio di analisi bayesiana dei dati che trovate nel mio programma di statistica Ministat, che può essere scaricato liberamente dall’area di download. 
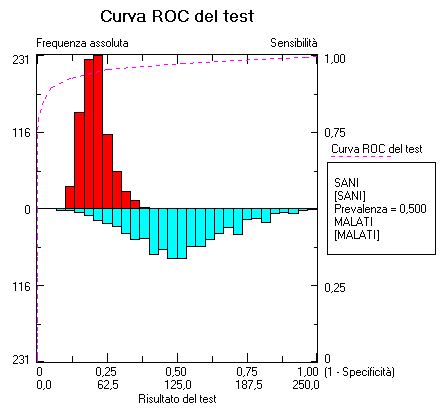Nella situazione ideale, di completa separazione dei valori del rumore da quelli del segnale abbiamo una curva ROC che sale perfettamente verticale sull'asse delle ordinate quindi piega ad angolo retto in orizzontale, parallela all'asse delle ascisse: 
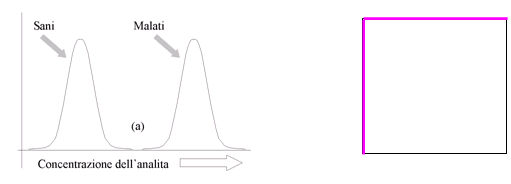Nella situazione opposta, di completa sovrapposizione dei valori del rumore e di quelli del segnale, nella quale segnale e rumore sono quindi indistinguibili l'uno dall'altro, abbiamo una curva ROC che è una retta che va dall'angolo inferiore sinistro all'angolo superiore destro: 
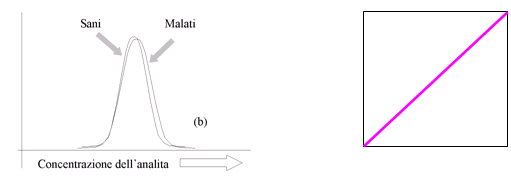Nella pratica (Zenone docet) si incontrano curve che giacciono in mezzo ai due estremi sopra riportati: 
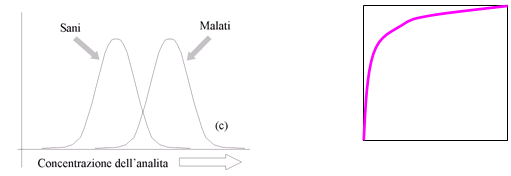L'area sottesa alla curva fornisce una misura delle prestazioni del radar (nell'esempio aeronautico) e del test di laboratorio (nel nostro caso). Il massimo valore di sensibilità è uguale a 1, e il massimo valore di (1- specificità) è uguale a 1, e pertanto l'area totale massima sottesa dalla curva è uguale a 1. Nel caso del radar l'area sottesa dalla curva rappresenta la probabilità che un aereo fornisca un segnale (radar) superiore a quello del rumore (di fondo). Nel caso del test diagnostico questa area rappresenta la probabilità che una persona con la malattia, presa a caso, abbia un risultato superiore a quello di una persona senza la malattia, presa a caso [2]. Se la curva ROC (del radar/del test di laboratorio) va dall'angolo inferiore sinistro all'angolo superiore destro la probabilità è uguale a 0,5: e l’informazione fornita dal radar/test di laboratorio è uguale a quella che si può ricavare dal lancio di una moneta! L’unico limite delle curve ROC deriva dal fatto che sono costruite a partire dalla sensibilità e dalla specificità, e non prendono in considerazione la probabilità a priori (prevalenza della malattia nel caso di un test diagnostico). Le curve ROC forniscono quindi una soluzione parziale, e per questo motivo non possono sostituire l'approccio bayesiano analitico (completo) che trovate nelle pagine di questo sito. Per contro le curve ROC forniscono un facile e immediato strumento per il confronto delle prestazioni di un radar/test di laboratorio nei confronti di un altro. Un radar le cui caratteristiche operative sono descritte da una curva che giace completamente al di sopra delle curva di un altro radar ha prestazioni migliori. Analogamente un test di laboratorio descritto da una curva che giace completamente al di sopra delle curva di un altro test ha prestazioni migliori [3]. In entrambi i casi l'area sottesa dalla curva è una misura dell'informazione che il radar/test di laboratorio è in grado di fornire: tanto maggiore è l’area, tanto maggiore è l’informazione fornita (e tanto migliori sono il radar e il test di laboratorio). Due sono i risultati notevoli. Il primo è rappresentato dal fatto che la stessa soluzione è stata trovata partendo da problemi così diversi quali l’interpretazione di un segnale radar e l’interpretazione del risultato di un test di laboratorio: e questa non è che l’ennesima riprova dello straordinario, quasi “magico” potere esplicativo della matematica [4], [5]. Il secondo è rappresentato dal fatto che è possibile misurare l’informazione fornita da un test diagnostico sintetizzandola in un unico valore: cosa che rende possibile confrontare tra di loro le accuratezze diagnostiche di test differenti per la stessa malattia [3] in modo oggettivo. Se ci pensate, non si tratta di risultati da poco. ********************************
L’esempio riportato, che si riferisce ad un ottimo test diagnostico (sensibilità e specificità entrambe pari al 95%), è paradigmatico. Lo scarso valore aggiunto, in termini di informazione, che i marcatori tumorali forniscono alla diagnosi, rappresenta il razionale per cui se ne sconsiglia l’uso come test di screening in una popolazione non selezionata. Il teorema di Bayes rappresenta l'unico strumento che consente di fornire una misura quantitativa, e quindi oggettiva, espressa in termini di informazione, del valore aggiunto fornito da un test diagnostico. Dal punto di vista epistemologico risultano evidenti nel teorema di Bayes:→ la capacità di formalizzare il meccanismo con cui si ribaltare la logica, da l’effetto|data la causa a la causa|dato l’effetto, passando dalla deduzione all’induzione (che risulta per definizione solo probabile);→ la capacità di formalizzare il meccanismo con cui l’informazione fornita dall’esperienza (lo specifico risultato del test di laboratorio) si somma all’informazione a priori, aumentando la nostra conoscenza;→ la capacità di misurare l’informazione che un test diagnostico fonisce alla diagnosi medica [a]. Dal punto di vista pratico risulta evidente dal teorema di Bayes che:→ in condizioni di bassa prevalenza diminuisce il valore predittivo del test positivo;→ in condizioni di bassa specificità del test diminuisce il valore predittivo del test positivo;→ in condizioni di bassa specificità e di bassa prevalenza aumenta il valore predittivo del test negativo, quindi un test diventa utile soprattutto per escludere la malattia. Questi argomenti sono ulteriormente trattati nelle prossime parti. In particolare per quanto riguarda la capacità del teorema di Bayes di formalizzare il meccanismo con cui l’informazione fornita dall’esperienza (lo specifico risultato del test di laboratorio) si somma all’informazione a priori, aumentando la nostra conoscenza, vedremo come, in alternativa all’interpretazione frequentista qui illustrata, nella quale la probabilità a priori è rappresentata dalla prevalenza della malattia, sia possibile adottare un approccio “soggettivista”, forse per alcuni aspetti più vicino al modo di ragionare del clinico. Inoltre verranno approfondite ulteriormente le conseguenze della bassa specificità di un test di laboratorio e della bassa prevalenza della malattia. Per le definizioni di base rimando anche alle Statistics Notes di Altman nella pagina iniziale del teorema di Bayes. Ho riassunto gli argomenti trattati in questa parte in una presentazione, dal titolo teorema di Bayes e informazione diagnostica. Informazione diagnostica e curve ROC ROC è l'acronimo di Receiver Operating Characteristic (caratteristiche operative del ricevitore) e ha un’origine che vale la pena di ricordare. Perchè il ricevitore in questione è il radar. Durante la seconda guerra mondiale il problema era, nell'ambito del rumore di fondo presente nei segnali radar, riconoscere il segnale causato dalla presenza di oggetti nemici sui campi di battaglia (tipicamente nei cieli, ma anche in mare). Si tratta di un classico problema di rapporto segnale/rumore [b] che è stato affrontato dagli ingegneri nell'ambito della teoria della rilevazione del segnale. Vediamo un primo esempio numerico, rappresentato dalla seguente serie di dati: 3, 4, 6, 2, 6, 5, 4, 5, 3, 3, 6, 12, 4, 5, 6, 6, 7, 4, 5, 4, 4, 4, 3, 5, 11, 3, 3, 5, 2, 5, 4, 3, 2 Supponiamo di avere un filtro digitale (in realtà negli anni '40 del secolo scorso si avevano a disposizione dati analogici e filtri analogici, ma concettualmente la situazione è identica), un filtro che possa essere variato in continuo, ponendo la prima volta la soglia a 12, e considerando "rumore" i valori inferiori a 12 e "segnale" i valori uguali o superiori a 12, ponendo la seconda volta la soglia a 11, e considerando "rumore" i valori inferiori a 11 e "segnale" i valori uguali o superiori a 11, e così via. Dopo avere filtrato il segnale utilizzando tutte le possibili soglie (gli interi compresi tra 12 e 2) otteniamo la seguente serie di dati (il rumore viene posto convenzionalmente uguale a “_”): _, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, 7, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, 6, _, 6, _, _, _, _, _, 6, 12, _, _, 6, 6, 7, _, _, _, _, _, _, _, 11, _, _, _, _, _, _, _, __, _, 6, _, 6, 5, _, 5, _, _, 6, 12, _, 5, 6, 6, 7, _, 5, _, _, _, _, 5, 11, _, _, 5, _, 5, _, _, __, 4, 6, _, 6, 5, 4, 5, _, _, 6, 12, 4, 5, 6, 6, 7, 4, 5, 4, 4, 4, _, 5, 11, _, _, 5, _, 5, 4, _, _3, 4, 6, _, 6, 5, 4, 5, 3, 3, 6, 12, 4, 5, 6, 6, 7, 4, 5, 4, 4, 4, 3, 5, 11, 3, 3, 5, _, 5, 4, 3, _3, 4, 6, 2, 6, 5, 4, 5, 3, 3, 6, 12, 4, 5, 6, 6, 7, 4, 5, 4, 4, 4, 3, 5, 11, 3, 3, 5, 2, 5, 4, 3, 2 Supponendo che i segnali di intensità 11 e 12 provengano dagli oggetti che volevamo rilevare (quindi, nell'esempio aeronautico, da due aerei), abbiamo individuato ciò che ci interessava in mezzo al rumore di fondo del radar (valori da 7 in giù). In questo esempio, come avete notato, mancano completamente i valori 8, 9 e 10. Il “rapporto segnale/rumore” (11 o 12 di segnale, contro 7 o meno di rumore) è elevato: e questo rende “evidente” la soglia tra rumore e segnale (il legame che intercorre tra valore soglia prescelto, che qui potrebbe essere 8, 9, 10 o 11, e sensibilità e specificità, è discusso nella parte su Teorema di Bayes e strategie diagnostiche). Ma la realtà è sempre fastidiosamente ambigua, e nella pratica si ha a che fare con distribuzioni dei valori che assomigliano di più a quella riportata in questo secondo esempio: 3, 4, 6, 2, 6, 9, 5, 4,10, 8, 10, 8, 5, 9, 6, 12, 11, 4, 7, 6, 8, 9, 3, 3, 5, 9, 12, 10, 4, 6, 7, 8, 6, 5, 4 Dopo avere filtrato il segnale utilizzando tutte le possibili soglie (interi compresi tra 12 e 2) otteniamo ora la seguente serie di dati: _, _, _, _, _, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, _, _, _, _, _, _, _, 12, 11, _, _, _, _, _, _, _, _, _, 12, _, _, _, _, _, _, _, __, _, _, _, _, _, _, _, 10, _, 10, _, _, _, _, 12, 11, _, _, _, _, _, _, _, _, _, 12, 10, _, _, _, _, _, _, __, _, _, _, _, 9, _, _, 10, _, 10, _, _, 9, _, 12, 11, _, _, _, _, 9, _, _, _, 9, 12, 10, _, _, _, _, _, _, __, _, _, _, _, 9, _, _, 10, 8, 10, 8, _, 9, _, 12, 11, _, _, _, 8, 9, _, _, _, 9, 12, 10, _, _, _, 8, _, _, __, _, _, _, _, 9, _, _, 10, 8, 10, 8, _, 9, _, 12, 11, _, 7, _, 8, 9, _, _, _, 9, 12, 10, _, _, 7, 8, _, _, __, _, 6, _, 6, 9, _, _, 10, 8, 10, 8, _, 9, 6, 12, 11, _, 7, 6, 8, 9, _, _, _, 9, 12, 10, _, 6, 7, 8, 6, _, __, _, 6, _, 6, 9, 5, _, 10, 8, 10, 8, 5, 9, 6, 12, 11, _, 7, 6, 8, 9, _, _, 5, 9, 12, 10, _, 6, 7, 8, 6, 5, __, 4, 6, _, 6, 9, 5, 4, 10, 8, 10, 8, 5, 9, 6, 12, 11, 4, 7, 6, 8, 9, _, _, 5, 9, 12, 10, 4, 6, 7, 8, 6, 5, 43, 4, 6, _, 6, 9, 5, 4, 10, 8, 10, 8, 5, 9, 6, 12, 11, 4, 7, 6, 8, 9, 3, 3, 5, 9, 12, 10, 4, 6, 7, 8, 6, 5, 43, 4, 6, 2, 6, 9, 5, 4, 10, 8, 10, 8, 5, 9, 6, 12, 11, 4, 7, 6, 8, 9, 3, 3, 5, 9, 12, 10, 4, 6, 7, 8, 6, 5, 4 Il problema è che questa volta i valori variano da 2 a 12 senza soluzioni di continuo: e la soglia tra segnale e rumore non è più “evidente” come sembrava esserlo nel primo caso. Ci troviamo di fronte a una della infinite varianti del paradosso del sorite di Zenone: quale è il granello che fa passare un mucchio di sabbia in un non-mucchio? La cui forma in questo caso è: quale è il valore che segna la transizione da un segnale a un non-segnale, ovvero quale è il valore soglia al di sotto del quale dobbiamo pensare che non si tratti più di un segnale (un aereo), ma si tratti semplicemente di rumore di fondo? Questo secondo esempio illustra una situazione in cui il rapporto segnale/rumore è ridotto, e quindi abbiamo difficoltà a distiguere l'uno dall'altro. Gli ingegneri hanno modellizzato il problema trovando una generalizzazione che consente di affrontarlo "more scientifico". E come vedete anche nella Wikipedia [1] si tratta del modello utilizzato per la diagnostica di laboratorio e la diagnosi medica in generale. Nelle quali il risultato del test nei malati è il segnale, il risultato del test nei sani è il rumore (di fondo). E la curva ROC è costruita semplicemente riportando in ascisse la sensibilità e in ordinate (1 - specificità), come si può vedere nella figura seguente che è tratta dell’esempio di analisi bayesiana dei dati che trovate nel mio programma di statistica Ministat, che può essere scaricato liberamente dall’area di download. Nella situazione ideale, di completa separazione dei valori del rumore da quelli del segnale abbiamo una curva ROC che sale perfettamente verticale sull'asse delle ordinate quindi piega ad angolo retto in orizzontale, parallela all'asse delle ascisse: Nella situazione opposta, di completa sovrapposizione dei valori del rumore e di quelli del segnale, nella quale segnale e rumore sono quindi indistinguibili l'uno dall'altro, abbiamo una curva ROC che è una retta che va dall'angolo inferiore sinistro all'angolo superiore destro: Nella pratica (Zenone docet) si incontrano curve che giacciono in mezzo ai due estremi sopra riportati: L'area sottesa alla curva fornisce una misura delle prestazioni del radar (nell'esempio aeronautico) e del test di laboratorio (nel nostro caso). Il massimo valore di sensibilità è uguale a 1, e il massimo valore di (1- specificità) è uguale a 1, e pertanto l'area totale massima sottesa dalla curva è uguale a 1. Nel caso del radar l'area sottesa dalla curva rappresenta la probabilità che un aereo fornisca un segnale (radar) superiore a quello del rumore (di fondo). Nel caso del test diagnostico questa area rappresenta la probabilità che una persona con la malattia, presa a caso, abbia un risultato superiore a quello di una persona senza la malattia, presa a caso [2]. Se la curva ROC (del radar/del test di laboratorio) va dall'angolo inferiore sinistro all'angolo superiore destro la probabilità è uguale a 0,5: e l’informazione fornita dal radar/test di laboratorio è uguale a quella che si può ricavare dal lancio di una moneta! L’unico limite delle curve ROC deriva dal fatto che sono costruite a partire dalla sensibilità e dalla specificità, e non prendono in considerazione la probabilità a priori (prevalenza della malattia nel caso di un test diagnostico). Le curve ROC forniscono quindi una soluzione parziale, e per questo motivo non possono sostituire l'approccio bayesiano analitico (completo) che trovate nelle pagine di questo sito. Per contro le curve ROC forniscono un facile e immediato strumento per il confronto delle prestazioni di un radar/test di laboratorio nei confronti di un altro. Un radar le cui caratteristiche operative sono descritte da una curva che giace completamente al di sopra delle curva di un altro radar ha prestazioni migliori. Analogamente un test di laboratorio descritto da una curva che giace completamente al di sopra delle curva di un altro test ha prestazioni migliori [3]. In entrambi i casi l'area sottesa dalla curva è una misura dell'informazione che il radar/test di laboratorio è in grado di fornire: tanto maggiore è l’area, tanto maggiore è l’informazione fornita (e tanto migliori sono il radar e il test di laboratorio). Due sono i risultati notevoli. Il primo è rappresentato dal fatto che la stessa soluzione è stata trovata partendo da problemi così diversi quali l’interpretazione di un segnale radar e l’interpretazione del risultato di un test di laboratorio: e questa non è che l’ennesima riprova dello straordinario, quasi “magico” potere esplicativo della matematica [4], [5]. Il secondo è rappresentato dal fatto che è possibile misurare l’informazione fornita da un test diagnostico sintetizzandola in un unico valore: cosa che rende possibile confrontare tra di loro le accuratezze diagnostiche di test differenti per la stessa malattia [3] in modo oggettivo. Se ci pensate, non si tratta di risultati da poco. ********************************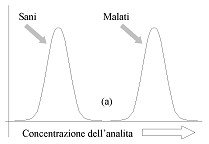 
|
|
|
|
|
|
||
|
||
|
|
|
|
Ultimo aggiornamento: 20 febbraio 2023
NOTA SUI COLLEGAMENTIALLE FONTI BIBLIOGRAFICHE La maggior parte dei collegamenti ad articoli scientifici riportati nel sito fa riferimento a riviste online che forniscono gratuitamente l’articolo originale. In alcuni casi è necessario registrarsi sul sito per avere libero accesso agli articoli: questo accade per esempio con il BMJ. Quando i collegamenti fanno riferimento a fonti bibliografiche a pagamento, chi non ha sottoscritto un abbonamento con la rivista potrebbe vedere comparire un messaggio del tipo “access forbidden”, ma il più delle volte vedrà comparire una pagina che consente di acquistare online l’articolo originale.
scelti per voi
Programma di statistica Ministat (versione per Windows)
Programma di statistica Open Source R(per Linux, Mac OS X e Windows)
Manuale Merck di diagnosie terapia
L’articolo da non perdere...
Errori congeniti del metabolismo
I migliori libri del mese Leonard Mlodinow La passeggiata dell’ubriaco. Le leggi scientifiche del caso.Rizzoli Editore, 2009, pp. 294ISBN: 17034081
OpenOffice, la suite Open Source (per Linux, Mac OS X e Windows)
ebooks... Mauss, Berg, Rockstroh, Sarrazin, Wedemeyer.Hepatology - A clinical textbook. 10th Edition - 2020
Le lettureconsigliate
Atlante di anatomia del Bock
Tavole metaboliche
Informazioni: info@bayes.itScrivimi: webmaster@bayes.it
NOTA LEGALE L’interpretazione dei risultati delle analisi di laboratorio deve essere effettuata esclusivamente dal medico e alla luce dei dati clinici.Questo sito ha uno scopo esclusivamente educativo e formativo. Pertanto le informazioni in esso contenute possono essere utilizzate esclusivamente a scopo didattico, e anche in questo caso sotto la responsabilità personale di chi le utilizza, sia per sé stesso sia per terzi.Le informazioni contenute in questo sito non possono e non devono essere utilizzate né a scopo diagnostico, né a scopo prognostico, né a scopo terapeutico, né per qualsiasi attività che abbia un impatto sia diretto sia indiretto sullo stato di salute di un individuo o di più individui.Nessuna responsabilità può essere imputata all’autore per danni diretti o indiretti e di qualsivoglia natura che potrebbero essere causati a sé stessi o a terzi a causa di errori, imprecisioni, omissioni, interpretazioni o utilizzo dei contenuti di questo sito o dei siti cui esso fa riferimento.
E ora che i test genetici sono alla portata di tutti?Con meno di mille euro è possibile comprare un test genetico su Internet: si manda un piccolo campione di cellule e poi si aspetta la risposta. Ma... a che cosa serve la risposta? Un dossier di Marika De Acetis dall’Archivio storico del sito www.torinoscienza.it
[Home] [Errori cognitivi] [Epistemologia] [Teorema di Bayes] [Decisioni mediche] [Le basi biochimiche][Analisi tradizionali] [Analisi genetiche] [Qualità in laboratorio] [Statistica e laboratorio][Storia delle medicina] [Download] [Link] [Bacheca] [FAQ] [Chi sono]
Attualità in tema di eGFR:
I migliori libri del mese Giovanni Federspil Logica clinica. I principi del metodo in medicina.McGraw-Hill, 2004, pp. 368ISBN: 88 386 2984-6
Atlante di virologia
Dal settembre 2008oltre 400 000 visitatori
ebooks... M. BesozziErrori cognitivi, probabilità e decisioni mediche. Fate click sul titolo o scaricate il testo su tablet o smartphone con il codice a barre riportato qui sotto. 
Atlante dei protozoi intestinali
Atlante di citologia e istologia
Statistica e grafica con R
Espressione dei risultati nel laboratorio di chimica clinica
Pathology outlines
Atlante di anatomia del Gray
Atlante di ematologia
Atlante di parassitologia
Micobatteriologia clinica
Concetti, metodi e strumenti per una
buona informazione
ebooks... M. BesozziStatistica e grafica con R Fate click sul titolo o scaricate il testo su tablet o smartphone con il codice a barre riportato qui sotto. 
I migliori libri del mese Luigi Tesio I bravi e i buoni.Perché la medicina clinica può essere una scienza.Il Pensiero Scientifico Editore, 2015, pp. 216 ISBN: 978-88-490-0538-7
Gli inganni della correlazione:
Storia delle unità di misura
Questo sito è stato archiviato ed è reso disponibile esclusivamente come memoria storica: pertanto è escluso ogni suo possibile utilizzo medico. Le parti del sito riservate al teorema di Bayes rimangono concettualmente valide, ma declino qualsiasi responsabilità per la lenta ma inevitabile obsolescenza dei restanti contenuti dovuta alla comparsa di nuove analisi di laboratorio, di progressi nelle analisi genetiche, di link interrotti, e quant’altro.
.