7. Teorema di Bayes e strategie diagnostiche
“Al mondo di sicuro ci sono solo la morte e le tasse.”(Benjamin Franklin) “L’importante è non smettere di farsi delle domande”(Albert Einstein)
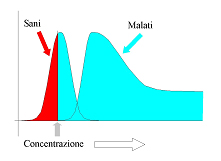
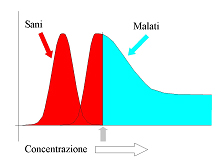
L’informazione prodotta dalla diagnostica di laboratorio non appartiene al novero delle cose “certe”. Ma, come abbiamo visto, appartiene al novero delle cose “misurabili”. Il che da alla diagnostica di laboratorio lo statuto di scienza (se pur una scienza applicata). Abbiamo anche visto come il teorema di Bayes rappresenta un approccio scientifico, e soprattutto quantitativo, in grado di misurare il contributo che la diagnostica di laboratorio fornisce alla diagnostica medica in termini di informazione: rendendo la diagnostica di laboratorio in questo modo ancora più “oggettivamente” utile di quanto, intuitivamente, essa appare. Ora si tratta di approfondire l’argomento sia dal punto di vista tecnico, sia dal punto di vista concettuale, cercando però sempre di ricavare dal nostro argomentare delle implicazioni pratiche. Per farlo, consideriamo come “sani” i pazienti con un risultato il cui valore cade a sinistra di una dato valore soglia di concentrazione, e come “malati” i pazienti con un risultato il cui valore cade a destra di un dato valore soglia di concentrazione. Partiamo dalla prima figura in alto, nella quale la distinzione tra sani e malati è stata fatta impiegando un valore soglia che consente, pur classificando un certo numero di sani come malati (falsi positivi), di classificare tutti i malati come tali: abbiamo privilegiato la sensibilità del test, a scapito della sua specificità. Nella seconda figura dall’alto, la distinzione tra sani e malati è stata fatta impiegando un valore soglia che consente, pur classificando un certo numero di malati come sani (falsi negativi), di classificare tutti i sani come tali: abbiamo privilegiato la specificità del test, a scapito della sua sensibilità.
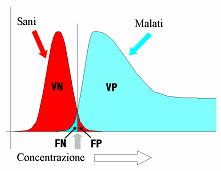
Infine nella terza figura dall’alto, la distinzione tra sani e malati è stata fatta impiegando un valore soglia che rappresenta un compromesso tra le due scelte precedenti. In particolare il valore soglia presescelto è quello che contemporaneamente massimizza i pazienti classificati correttamente (veri negativi VN e veri positivi VP) e minimizza i pazienti classificati in modo errato (falsi negativi FN e falsi positivi FP). Familiarizzare con l’analisi bayesiana dei dati Potete familiarizzare con queste tecniche e con questi concetti utilizzando l’esempio di analisi bayesiana dei dati che vi ho preparato, oppure utilizzando Ministat (potete scaricarlo dall’area di download). L’esempio si riferisce ai dati che potete trovare nel foglio BAYES del file ESEMPI.XLS che viene installata con Ministat. Si tratta di un campione simulato che include 853 soggetti sani e 853 malati, con una prevalenza della malattia del 50% (P = 0,5).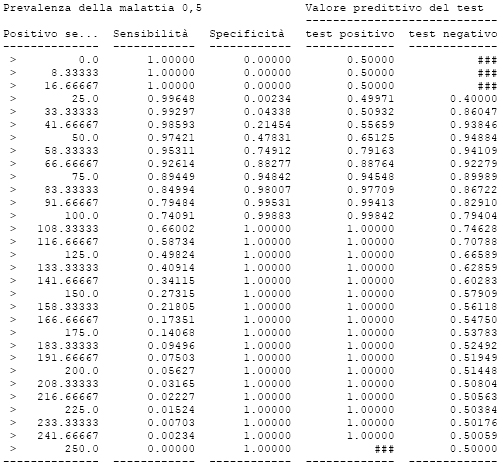 
Trovo sempre utili e didattiche le tabelle generate da Ministat che rappresentano le grandezze bayesiane in funzione dei valori di soglia. Infatti, per esempio, è sufficiente rianalizzare gli stessi dati imponendo una prevalenza della malattia dello 0,5% (o se preferite del 5 per mille, ovvero P = 0,005) per afferrare alcune proprietà molto importanti della grandezze bayesiane.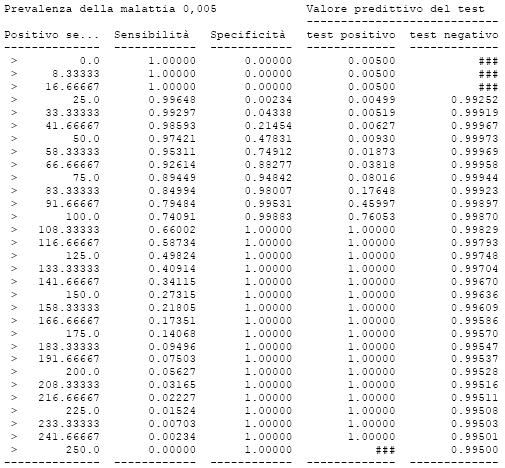 
Trovo sempre utili e didattiche le tabelle generate da Ministat che rappresentano le grandezze bayesiane in funzione dei valori di soglia. Infatti, per esempio, è sufficiente rianalizzare gli stessi dati imponendo una prevalenza della malattia dello 0,5% (o se preferite del 5 per mille, ovvero P = 0,005) per afferrare alcune proprietà molto importanti della grandezze bayesiane. La prima è che sensibilità e specificità non cambiano al variare della prevalenza. Una cosa che col senno di poi può, anzi deve risultare ovvia, ma che è didattico e consolante vedere ogni volta riprodursi davanti ai propri occhi. La seconda è che, a parità di valore soglia, al diminuire della prevalenza della malattia diminuisce il valore predittivo del test positivo (la probabilità di essere malato avendo un test positivo), mentre aumento il valore predittivo del test negativo (la probabilità di essere sano avendo un test negativo). La terza è che al diminuire della specificità di un test il valore predittivo del test positivo si avvicina progressivamente al valore della prevalenza o, in altre parole, quando la specificità tende a zero, il valore predittivo del test postivo tende al valore della prevalenza della malattia. Questa osservazione è molto importante se si pensa ad esempio ad un test molto aspecifico, come la velocità di eritrosedimentazione (VES). La VES risulta alterata in un numero così elevato di malattie che, per una data malattia, la sua specificità tende, appunto, a zero. Quindi di fronte per esempio al quesito specifico “quale è la probilità di avere l’artrite reumatoide avendo la VES alta?”, si ottiene un valore predittivo che è sostanzialmente uguale alla prevalenza della artrite reumatoide: ergo, la VES non ci fornisce alcun valore aggiunto in termini di informazione utile per una specifica diagnosi. Tuttavia accade, come avete visto, un fatto simmetrico: aumenta il valore predittivo del test negativo e se la malattia è abbastanza rara tale valore diventa una indicazione di “pratica certezza” per l’esclusione della malattia. Espressione alternativa del teorema di Bayes in termini di numeri naturali L’alternativa sulla quale insiste molto Gigerenzer [1], per la diagnostica di laboratorio è già stata affrontata in modo esaustivo in passato sia da Galen e Gambino sia da Gerhardt e Keller. Consiste nel sostituire ai valori di probabilità P i corrispondenti numeri interi (numeri naturali) nel modo che vi ho qui illustrato in dettaglio. Di fatto semplicemente moltiplicando le probabilità per le rispettive prevalenze si ottengono i valori numerici della tabella: VP = veri positivi, FN = falsi negativi, FP = falsi positivi, VN = veri negativi 
A questo punto è possibile a partire dal numero di casi osservati calcolare le grandezze bayesiane come:→ VP / (VP+FN) = sensibilità (positività del test nei malati);→ VN / (VN+FP) = specificità (negatività del test nei sani);→ (VP+FN) / (VP+FN+FP+VN) = prevalenza (numero dei malati);→ (VP / (VP+FP) = valore predittivo del test positivo (probabilità di essere malato se il test è positivo);→ VN / (VN+FN) = valore predittivo del test negativo (probabilità di essere sano se il test è negativo). Questo approccio corrisponde al percorso seguito quanto si raccolgono i risultati di un nuovo test di laboratorio in una casistica di soggetti affetti o non affetti da una specifica malattia, contando i casi da assegnare a ciascuna delle quattro caselle sopra individuate, per determinare appunto le caratteristiche di sensibilità e di specificità del test in questione. Uno strumento per effettuare con semplicità i calcoli necessari Con le espressioni riportate sopra possiamo calcolare i risultati dell’esempio tratto da Galen e Gambino [2] che si riferisce ai risultati della determinazione dell’alfa-fetoproteina nel cancro del fegato (malati) e in altri disordini (sani). I dati raccolti erano: 90 malati con il test positivo (VP), 2079 sani con il test negativo, (VN), 17 malati con il test negativo (FN), 39 sani con il test positivo (FP). Scaricate e aprite con Excel© o con OpenOffice.org© Calc il file “Bayes_num.xls” nelle celle da F2 a G3 vi ho mostrato come inserire i dati, che devono essere inseriti nelle celle corrispondenti de B2 a C3 sotto forma di numeri interi, cioè di casi osservati. Coerentemente con i calcoli sopra riportati, trovate che le grandezze bayesiane sono state calcolate rispettivamente come:→ sensibilità =B2/(B2+C2)→ specificità =C3/(C3+B3)→ prevalenza =(B2+C2)/SOMMA(B2:C3)→ valore predittivo del test positivo =B2/(B2+B3)→ valore predittivo del test negativo =C3/(C3+C2) Come vedete nel file la possibilità di disporre del numero di casi consente di calcolare per ciascuna di queste grandezze l’intervallo di confidenza (generalmente al 95%, ponendo z = 1,96, ma potete calcolarlo anche al 90% o al 99%, ponendo z rispettivamente uguale a 1,645 e 2,576). Si tratta di un punto cruciale, in quanto sia dal punto di vista epistemologico sia dal punto di vista metodologico è un “dovere scientifico” comunicare sempre il grado di incertezza che caratterizza l’informazione ottenuta. Pertanto la regola fondamentale è che qualsiasi conclusione statistica deve essere sempre accompagnata della misura dell’incertezza che la caratterizza, espressa sotto forma di intervallo di confidenza (vedere ad esempio in http://en.wikipedia.org/wiki/Confidence_interval). Il teorema di Bayes come ausilio per la definizione delle strategie diagnostiche Queste osservazioni introducono il concetto di strategia diagnostica a livello del singolo caso clinico. Se andate a rivedere il problema degli anticorpi anti-HIV (problema 7) vedete che il teorema di Bayes ci indica chiaramente come più economico e saggio eseguire ad un paziente prima gli anticorpi anti-HIV, anche se il valore predittivo del test positivo è “solamente” del 50% (cioè un paziente con anticorpi anti-HIV positivi ha il 50% di probabilità di essere malato, e reciprocamente ha il 50% di probabilità di essere sano: come dire che potremmo decidere se è sano e malato lanciando in aria una moneta!). Infatti i falsi positivi possono poi essere individuati successivamente mediante un test di secondo livello (western-blot), un test costoso, che però verrà praticato solamente al 6 per mille dei pazienti, mentre ai rimanenti ci si sarà limitati ad effettuare il test (assai meno costoso) degli anticorpi anti-HIV. Questa idea collega la strategia diagnostica individuale alla strategia diagnostica in termini di politica sanitaria. Qui l’argomento si fa un po più delicato, in quanto bisognerebbe poi valutare l’efficacia della strategia in termini di ricaduta sullo stato di salute della popolazione. Misurare l’efficacia della costruzione della fognature non ha richiesto la messa a punto di sofisticati indicatori statistici: l’efficacia è stata resa “evidente” dalla scomparsa delle epidemie di peste bubbonica. Anche l’efficacia della vaccinazioni è stato resa “evidente” dalla (ad esempio) scomparsa del vaiolo e della poliomelite. Ma già se abbiamo di fronte il caso della meningite meningococcica, la valutazione di efficacia diventa più difficile. Che dire poi di un test di screening per il sangue occulto nelle feci? Il teorema di Bayes ci consente quantomeno di misurare quello che accade/acccadrebbe in termini di veri positivi, falsi positivi, quindi di esiti per la salute. Su questi argomenti ho ripreso le argomentazioni sia di Galen e Gambino sia di Gerhardt e Keller, pure rendendomi conto del fatto che si tratta di un argomento difficile, che sarà necessario sviluppare ulteriormente. Ho riassunto gli argomenti trattati in questa parte anche in una presentazione, dal titolo teorema di Bayes e strategie diagnostiche. ********************************
A questo punto è possibile a partire dal numero di casi osservati calcolare le grandezze bayesiane come:→ VP / (VP+FN) = sensibilità (positività del test nei malati);→ VN / (VN+FP) = specificità (negatività del test nei sani);→ (VP+FN) / (VP+FN+FP+VN) = prevalenza (numero dei malati);→ (VP / (VP+FP) = valore predittivo del test positivo (probabilità di essere malato se il test è positivo);→ VN / (VN+FN) = valore predittivo del test negativo (probabilità di essere sano se il test è negativo). Questo approccio corrisponde al percorso seguito quanto si raccolgono i risultati di un nuovo test di laboratorio in una casistica di soggetti affetti o non affetti da una specifica malattia, contando i casi da assegnare a ciascuna delle quattro caselle sopra individuate, per determinare appunto le caratteristiche di sensibilità e di specificità del test in questione. Uno strumento per effettuare con semplicità i calcoli necessari Con le espressioni riportate sopra possiamo calcolare i risultati dell’esempio tratto da Galen e Gambino [2] che si riferisce ai risultati della determinazione dell’alfa-fetoproteina nel cancro del fegato (malati) e in altri disordini (sani). I dati raccolti erano: 90 malati con il test positivo (VP), 2079 sani con il test negativo, (VN), 17 malati con il test negativo (FN), 39 sani con il test positivo (FP). Scaricate e aprite con Excel© o con OpenOffice.org© Calc il file “Bayes_num.xls” nelle celle da F2 a G3 vi ho mostrato come inserire i dati, che devono essere inseriti nelle celle corrispondenti de B2 a C3 sotto forma di numeri interi, cioè di casi osservati. Coerentemente con i calcoli sopra riportati, trovate che le grandezze bayesiane sono state calcolate rispettivamente come:→ sensibilità =B2/(B2+C2)→ specificità =C3/(C3+B3)→ prevalenza =(B2+C2)/SOMMA(B2:C3)→ valore predittivo del test positivo =B2/(B2+B3)→ valore predittivo del test negativo =C3/(C3+C2) Come vedete nel file la possibilità di disporre del numero di casi consente di calcolare per ciascuna di queste grandezze l’intervallo di confidenza (generalmente al 95%, ponendo z = 1,96, ma potete calcolarlo anche al 90% o al 99%, ponendo z rispettivamente uguale a 1,645 e 2,576). Si tratta di un punto cruciale, in quanto sia dal punto di vista epistemologico sia dal punto di vista metodologico è un “dovere scientifico” comunicare sempre il grado di incertezza che caratterizza l’informazione ottenuta. Pertanto la regola fondamentale è che qualsiasi conclusione statistica deve essere sempre accompagnata della misura dell’incertezza che la caratterizza, espressa sotto forma di intervallo di confidenza (vedere ad esempio in http://en.wikipedia.org/wiki/Confidence_interval). Il teorema di Bayes come ausilio per la definizione delle strategie diagnostiche Queste osservazioni introducono il concetto di strategia diagnostica a livello del singolo caso clinico. Se andate a rivedere il problema degli anticorpi anti-HIV (problema 7) vedete che il teorema di Bayes ci indica chiaramente come più economico e saggio eseguire ad un paziente prima gli anticorpi anti-HIV, anche se il valore predittivo del test positivo è “solamente” del 50% (cioè un paziente con anticorpi anti-HIV positivi ha il 50% di probabilità di essere malato, e reciprocamente ha il 50% di probabilità di essere sano: come dire che potremmo decidere se è sano e malato lanciando in aria una moneta!). Infatti i falsi positivi possono poi essere individuati successivamente mediante un test di secondo livello (western-blot), un test costoso, che però verrà praticato solamente al 6 per mille dei pazienti, mentre ai rimanenti ci si sarà limitati ad effettuare il test (assai meno costoso) degli anticorpi anti-HIV. Questa idea collega la strategia diagnostica individuale alla strategia diagnostica in termini di politica sanitaria. Qui l’argomento si fa un po più delicato, in quanto bisognerebbe poi valutare l’efficacia della strategia in termini di ricaduta sullo stato di salute della popolazione. Misurare l’efficacia della costruzione della fognature non ha richiesto la messa a punto di sofisticati indicatori statistici: l’efficacia è stata resa “evidente” dalla scomparsa delle epidemie di peste bubbonica. Anche l’efficacia della vaccinazioni è stato resa “evidente” dalla (ad esempio) scomparsa del vaiolo e della poliomelite. Ma già se abbiamo di fronte il caso della meningite meningococcica, la valutazione di efficacia diventa più difficile. Che dire poi di un test di screening per il sangue occulto nelle feci? Il teorema di Bayes ci consente quantomeno di misurare quello che accade/acccadrebbe in termini di veri positivi, falsi positivi, quindi di esiti per la salute. Su questi argomenti ho ripreso le argomentazioni sia di Galen e Gambino sia di Gerhardt e Keller, pure rendendomi conto del fatto che si tratta di un argomento difficile, che sarà necessario sviluppare ulteriormente. Ho riassunto gli argomenti trattati in questa parte anche in una presentazione, dal titolo teorema di Bayes e strategie diagnostiche. ******************************** |
|
|
|
|
|
||
|
||
|
|
|
|
Ultimo aggiornamento: 20 febbraio 2023
NOTA SUI COLLEGAMENTIALLE FONTI BIBLIOGRAFICHE La maggior parte dei collegamenti ad articoli scientifici riportati nel sito fa riferimento a riviste online che forniscono gratuitamente l’articolo originale. In alcuni casi è necessario registrarsi sul sito per avere libero accesso agli articoli: questo accade per esempio con il BMJ. Quando i collegamenti fanno riferimento a fonti bibliografiche a pagamento, chi non ha sottoscritto un abbonamento con la rivista potrebbe vedere comparire un messaggio del tipo “access forbidden”, ma il più delle volte vedrà comparire una pagina che consente di acquistare online l’articolo originale.
scelti per voi
Programma di statistica Ministat (versione per Windows)
Programma di statistica Open Source R(per Linux, Mac OS X e Windows)
Manuale Merck di diagnosie terapia
L’articolo da non perdere...
Errori congeniti del metabolismo
I migliori libri del mese Leonard Mlodinow La passeggiata dell’ubriaco. Le leggi scientifiche del caso.Rizzoli Editore, 2009, pp. 294ISBN: 17034081
OpenOffice, la suite Open Source (per Linux, Mac OS X e Windows)
ebooks... Mauss, Berg, Rockstroh, Sarrazin, Wedemeyer.Hepatology - A clinical textbook. 10th Edition - 2020
Le lettureconsigliate
Atlante di anatomia del Bock
Tavole metaboliche
Informazioni: info@bayes.itScrivimi: webmaster@bayes.it
NOTA LEGALE L’interpretazione dei risultati delle analisi di laboratorio deve essere effettuata esclusivamente dal medico e alla luce dei dati clinici.Questo sito ha uno scopo esclusivamente educativo e formativo. Pertanto le informazioni in esso contenute possono essere utilizzate esclusivamente a scopo didattico, e anche in questo caso sotto la responsabilità personale di chi le utilizza, sia per sé stesso sia per terzi.Le informazioni contenute in questo sito non possono e non devono essere utilizzate né a scopo diagnostico, né a scopo prognostico, né a scopo terapeutico, né per qualsiasi attività che abbia un impatto sia diretto sia indiretto sullo stato di salute di un individuo o di più individui.Nessuna responsabilità può essere imputata all’autore per danni diretti o indiretti e di qualsivoglia natura che potrebbero essere causati a sé stessi o a terzi a causa di errori, imprecisioni, omissioni, interpretazioni o utilizzo dei contenuti di questo sito o dei siti cui esso fa riferimento.
E ora che i test genetici sono alla portata di tutti?Con meno di mille euro è possibile comprare un test genetico su Internet: si manda un piccolo campione di cellule e poi si aspetta la risposta. Ma... a che cosa serve la risposta? Un dossier di Marika De Acetis dall’Archivio storico del sito www.torinoscienza.it
[Home] [Errori cognitivi] [Epistemologia] [Teorema di Bayes] [Decisioni mediche] [Le basi biochimiche][Analisi tradizionali] [Analisi genetiche] [Qualità in laboratorio] [Statistica e laboratorio][Storia delle medicina] [Download] [Link] [Bacheca] [FAQ] [Chi sono]
Attualità in tema di eGFR:
I migliori libri del mese Giovanni Federspil Logica clinica. I principi del metodo in medicina.McGraw-Hill, 2004, pp. 368ISBN: 88 386 2984-6
Atlante di virologia
Dal settembre 2008oltre 400 000 visitatori
ebooks... M. BesozziErrori cognitivi, probabilità e decisioni mediche. Fate click sul titolo o scaricate il testo su tablet o smartphone con il codice a barre riportato qui sotto. 
Atlante dei protozoi intestinali
Atlante di citologia e istologia
Statistica e grafica con R
Espressione dei risultati nel laboratorio di chimica clinica
Pathology outlines
Atlante di anatomia del Gray
Atlante di ematologia
Atlante di parassitologia
Micobatteriologia clinica
Concetti, metodi e strumenti per una
buona informazione
ebooks... M. BesozziStatistica e grafica con R Fate click sul titolo o scaricate il testo su tablet o smartphone con il codice a barre riportato qui sotto. 
I migliori libri del mese Luigi Tesio I bravi e i buoni.Perché la medicina clinica può essere una scienza.Il Pensiero Scientifico Editore, 2015, pp. 216 ISBN: 978-88-490-0538-7
Gli inganni della correlazione:
Storia delle unità di misura
Questo sito è stato archiviato ed è reso disponibile esclusivamente come memoria storica: pertanto è escluso ogni suo possibile utilizzo medico. Le parti del sito riservate al teorema di Bayes rimangono concettualmente valide, ma declino qualsiasi responsabilità per la lenta ma inevitabile obsolescenza dei restanti contenuti dovuta alla comparsa di nuove analisi di laboratorio, di progressi nelle analisi genetiche, di link interrotti, e quant’altro.
.