5. Complessità, probabilità e teorema di Bayes
“Il concetto di probabilità è il più importante della scienza moderna, soprattutto perché nessuno ha la più pallida idea del suo significato.”(Bertrand Russel) “La probabilità: chi è costei? Prima di rispondere a tale domanda è certamente opportuno chiedersi: ma davvero “esiste” la probabilità? e cosa mai sarebbe? Io risponderei di no, che non esiste.”(Bruno de Finetti) Il secondo dei due fattori chiave per “la qualità della conoscenza” è rappresentato dalla qualità delle regole: si devono sapere, devono esser giuste e devono essere applicate correttamente le regole. Ma quali regole? Il problema cruciale è, come abbiamo visto, essere costretti a decidere in condizioni di incertezza. E poiché questa, come abbiamo capito, risulta ineliminabile dalla scelte umane, la sola cosa che possiamo ragionevolmente fare per non subirla è imparare a gestirla. Come? Andando alla ricerca delle regole del pre-vedere (vedere prima). Ma già la ricerca delle regole per prevedere un risultato banale (testa o croce) come quello del lancio di una moneta ci fa scontrare contro un concetto irriducibile: il caso. Per affrontare il problema l’unica possibilità è, come dicono Russel e De Finetti, di opporgli un concetto altrettanto irriducibile: la probabilità. La matematica ha trovato, per un evidente ossimoro, la ricerca delle regole del caso, l’unica soluzione scientifica possibile. I filosofi della scienza attribuiscono al termine probabilità due significati o valori: e parlano di probabilità epistemica e di probabilità non epistemica. Probabilità epistemica Nel caso di processi probabilistici nei quali la probabilità risulta epistemica, si ha a che fare con conclusioni che vengono espresse in modo probabilistico a causa della nostra ignoranza sullo stato reale del sistema in esame. Come ricordato da Ghirardi [1], il concetto di probabilità epistemica rispecchia perfettamente la posizione meccanicistica del grande matematico francese Simon de Laplace, che nel 1776 scriveva “Lo stato attuale del sistema della natura consegue evidentemente da quello che esso era nell’istante precedente, e se noi immaginassimo un’intelligenza che ad un dato istante comprendesse tutte le relazioni fra le entità di questo universo, esso potrebbe conoscere le rispettive posizioni, i moti e le disposizioni generali di tutte quelle entità in qualunque istante del passato e del futuro… Ma l’ignoranza delle diverse cause che concorrono alla formazione degli eventi come pure la loro complessità, insieme coll’imperfezione dell’analisi, ci impediscono di conseguire la stessa certezza rispetto alla grande maggioranza dei fenomeni. Vi sono quindi cose che per noi sono incerte, cose più o meno probabili, e noi cerchiamo di rimediare all’impossibilità di conoscerle determinando i loro diversi gradi di verosimiglianza. Accade così che alla debolezza della mente umana si debba una delle più fini e ingegnose fra le teorie matematiche, la scienza del caso o della probabilità”. Secondo Laplace, note le posizioni e le velocità di tutte le particelle dell’universo, e le leggi che ne governano i rapporti, sarebbe stato possibile prevederne l’evoluzione per l’eternità. La concezione di Laplace configura la probabilità nella descrizione dei processi fisici come accidentale, legata alla nostra ignoranza, ma in linea di principio eludibile. Come ancora ci ricorda Ghirardi [1], nel 1903 il grande matematico, fisico e filosofo della scienza Henri Poincarè scriveva: “Una causa piccolissima che sfugga alla nostra attenzione determina un effetto considerevole, che non possiamo mancare di vedere, e allora diciamo che l’effetto è dovuto al caso. Se conoscessimo esattamente le leggi della natura e la situazione dell’universo all’istante iniziale, potremmo prevedere esattamente la situazione dello stesso universo in un istante successivo. Ma se pure accadesse che le leggi naturali non avessero più alcun segreto per noi, anche in tal caso potremmo conoscere la situazione iniziale solo approssimativamente. Se questo ci permettesse di prevedere la situazione successiva con la stessa approssimazione non ci occorrerebbe di più e dovremmo dire che il fenomeno è stato previsto, che è governato da leggi. Ma non sempre è così: può accadere che piccole differenze nelle condizioni iniziali ne producano di grandissime nei fenomeni finali. Un piccolo errore nelle prime produce un errore enorme nei secondi. La previsione diviene impossibile, e si ha un fenomeno fortuito”. L’estrema sensibilità alle condizioni iniziali descritta da Poincarè, apre la strada ai moderni concetti di “caos deterministico” e di “complessità”. Laddove nella sua accezione più generale il concetto di complessità pone in crisi l’idea che in ogni caso lo studio dei sistemi complessi possa ricondursi allo studio dei loro costituenti. Come commenta Ghirardi “di fatto risulta relativamente facile dimostrare che esistono sistemi deterministici [come il banale lancio di una moneta, N.d.A.] con una tale sensibilità alle condizioni iniziali che la previsione del loro comportamento anche dopo tempi brevi richiederebbe una tale massa di informazioni (proprio perché le imprecisioni iniziali si amplificano esponenzialmente) che non potrebbero venire immagazzinate neppure in un computer che utilizzasse come chips tutte le particelle dell’universo e potesse immagazzinare un bit in ogni chip. La conclusione è che ci si è resi conto (e questo rappresenta indubbiamente una notevole conquista concettuale) che non sono rare situazioni in cui risulta di fatto impossibile prevedere il comportamento di un sistema per un periodo di tempo anche ragionevolmente breve… Il fatto che se anche tutto l’universo diventasse un calcolatore esso non risulterebbe abbastanza potente da permetterci di immagazzinare le informazioni necessarie a prevedere per più di qualche minuto l’evoluzione di un semplice sistema, non toglie nulla al fatto che secondo lo schema teorico che si è assunto soggiacere alla dinamica del processo, la necessità di ricorrere ad una descrizione probabilistica deriva dall’ignoranza circa le precise condizioni iniziali… Al contrario nelle schema quantomeccanico…l’aleatorietà degli esiti è incorporata nella struttura stesa del formalismo che, se assunto come completo, non consente neppure di pensare che, in generale, gli esiti siano, anche se in un modo a noi sconosciuto, predeterminati”. La meccanica quantistica introduce il concetto di probabilità non epistemica, cioè di descrizione probabilistica degli eventi che non può essere attribuita ad ignoranza. In altre parole, la descrizione probabilistica degli eventi non può essere attribuita ad una mancanza di informazioni sul sistema che, se fosse disponibile, ci consentirebbe di trasformare le asserzioni probabilistiche in asserzioni certe. I processi fisici microscopici sono fondamentalmente stocastici, e hanno una intrinseca e irriducibile aleatorietà. Probabilità non epistemica Riporto a questo proposito poche frasi dalla presentazione del volume de “Le Scienze” curato da Casati [2] nella quale il curatore, tra le altre cose, dice: “…è interessante osservare che la meccanica quantistica è una teoria intrinsecamente probabilistica. Una volta assegnato lo stato di un sistema al tempo t mediante una “funzione di stato” (t) noi siamo in grado di fare affermazioni solamente sulla probabilità che eseguendo una misura su una data grandezza si ottenga un determinato valore. Tuttavia è diverso il discorso relativo alla previsione della evoluzione futura. Infatti in meccanica quantistica lo stato (t) del sistema al tempo t è determinato univocamente dallo stato iniziale (0). Problema: siamo in grado, date le leggi del moto e dato (0), di determinare (t)? Il fatto straordinariamente inaspettato è che, a differenza della meccanica classica, la risposta a questa domanda è positiva: per i sistemi quantistici è possibile, almeno in linea di principio, risolvere le equazioni del moto e predire lo stato futuro (t). Pertanto il quadro che si va delineando è diametralmente opposto a quello che si aveva in precedenza: la meccanica classica è sempre stata considerata come una teoria deterministica; ora abbiamo visto che, a causa dell’insorgere del moto caotico, essa porta ad un comportamento statistico. D’altro lato la meccanica quantistica è intrinsecamente probabilistica; tuttavia, grazie al suo carattere di stabilità, risulta essere più predicibile della meccanica classica… La domanda che il lettore certamente si pone è quali implicazioni può avere lo studio del caos. In altri termini, a quale utilità pratica può portare il sapere che il comportamento della gran arte dei sistemi deterministici è in realtà così complicato da apparire completamente caotico, e che quindi essi si sottraggono alla nostra capacità di previsione? Anzitutto abbiamo imparato una lezione molto importante: leggi semplici non portano necessariamente a comportamenti semplici. Sarebbe alquanto vantaggioso se questo concetto fosse tenuto presente non solo nelle discipline scientifiche, ma anche nella vita politica ed economica. Un’altra lezione è che variazioni piccole nei parametri di un qualunque sistema non portano, necessariamente, a variazioni piccole nel “risultato”, cioè nella evoluzione futura: per esempio un aumento del 5% nell’inquinamento non sempre porta a un peggioramento solo del 5% nel danno ecologico. Una delle caratteristiche dello studio dei fenomeni caotici è la enorme potenzialità di una unificazione culturale in cui tutta la “filosofia naturale” e le discipline economiche, umanistiche, politiche e sociali sono coinvolte. La natura stessa sembra usare il caos nel suo programma di evoluzione: ogni schema deterministico fallirebbe se utilizzato per la sopravvivenza delle forme di vita in condizioni ambientali in continua trasformazione; la natura pertanto genera una quantità enorme di forme di vita attraverso mutazioni casuali e, da questa ampia possibilità di scelta, la selezione naturale trova candidati che si adattano alle mutate condizioni ambientali… tutte le volte che nel suo faticoso ed esaltante cammino verso la comprensione dei fenomeni naturali, l’uomo si è trovato di fronte a delle limitazioni, ciò è stato l’occasione per nuovi grandi balzi in avanti che hanno comportato un rovesciamento della filosofia precedente. Mi riferisco alla osservazione del valore limite della velocità della luce (che ha portato alla teoria della relatività), alla limitazione sulla precisione delle nostre misure (che ha portato alla meccanica quantistica); la teoria del caos ci ha messo di fronte a una limitazione ancora maggiore: l’impossibilità di prevedere il futuro…”. Brevi cenni sulla probabilità La teoria della probabilità parte dai giochi, e precisamente dagli studi pionieristici contenuti nel “Liber de ludo aleae” di G. Cardano (1501-1576) e nell’opera “Sopra le scoperte de li dadi” di G. Galilei (1564-1642). Anche se sono le questioni poste dal cavaliere De Merè (noto giocatore d'azzardo del XVII secolo) e le risposte fornite da B. Pascal (1623-1662) e P. De Fermat (1601-1665) a fondare il calcolo delle probabilità. Fino al ‘700 è quello che viene definito “il problema classico” a dominare l’attenzione. Abbiamo un’urna contenente 500 palline di colore bianco e 500 palline di colore rosso. Cosa ci possiamo attendere dall’estrazione di una pallina? Si sa tutto sull’urna, ovvero si conosce “l’universo”, ovvero si conosce la causa. Si applica un ragionamento deduttivo. Il risultato (l’effetto, l’estrazione di una pallina) può essere calcolato. Ma nel 1763 viene pubblicato postumo il saggio di Bayes, che indica la soluzione de “il problema inverso”. Da un’urna contenente s palline estraiamo n palline di cui k sono di colore rosso. Cosa possiamo concludere circa il contenuto dell’urna? Si è fatto un esperimento, si conosce l’effetto. Il problema che Bayes si pone è: esiste un qualche ragionamento induttivo che ci consenta di “calcolare” la causa (lo specifico contenuto dell’urna?).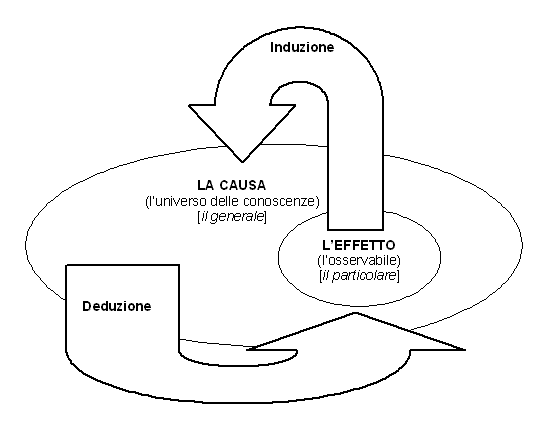 
Il matematico francese Pierre-Simon Laplace (1749-1827) riscopre ed estende questo risultato in un saggio del 1774, apparentemente ignaro dei risultati di Bayes. Bayes e Laplace rispondono così in linguaggio matematico al vecchio problema di Hume: sorgerà il sole domani? Immaginiamo un alieno che arrivi sulla terra, di notte. L'indomani vede per la prima volta sorgere il sole: quindi lo vede tramontare e scomparire. Chiediamogli che grado di fiducia ripone nel verificarsi dell'evento ricomparsa del sole. Non avendo alcuna altra informazione, la sola risposta ragionevole è 1/2: la probabilità che sorga, e la probabilità che non sorga, sono per lui, a priori, uguali. Ma l’indomani vede il sole sorgere una seconda volta. Quindi il terzo giorno lo vede sorgere ancora, e così via. Chiediamogli ogni volta che grado di fiducia ripone nel verificarsi dell'evento ricomparsa del sole. La soluzione, dopo n giorni, è P = (n+1) / (n+2) (5.1) mentre più in generale per il problema dell’urna contenente s palline dalla quale estraiamo n palline di cui k sono di colore rosso la probabilità che la prossima pallina sia rossa è P = (k+1) / (n+2) (5.2) I due fatti notevoli sono che la probabilità P non dipende da s, e che il valore di P tende a 1 ma non potrà mai raggiungere esattamente tale valore. Quindi l’induzione non potrà mai essere certa. Si consideri uno schema come il seguente, nel quale C rappresenta una delle tante cause osservabili, E rappresenta uno dei tanti effetti osservabili, e le frecce dirette dalla causa all’effetto rappresentano i rapporti di causa/effetto. 
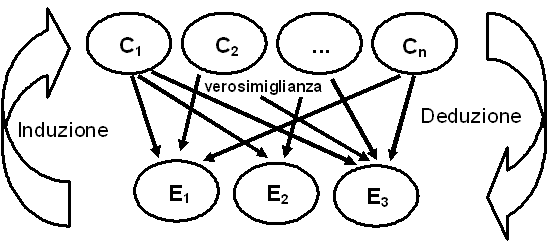Il problema classico può essere risolto applicando la deduzione. Conoscendo le cause, possiamo da queste dedurre gli effetti corrispondenti. La soluzione del problema inverso, ovvero l’induzione, è oltremodo più difficile, in quanto ad un effetto possono corrispondere più cause. Il teorema di Bayes consente, a partire dagli effetti osservati, di calcolare la verosimiglianza delle cause, espressa ovviamente nell’unico modo possibile: in termini di probabilità. Fatte queste premesse di tipo epistemologico e di tipo storico, è possibile affrontare l’argomento. Per scoprire subito che, sempre in onore ai motti di Russel e De Finetti, sono oggi ben quattro le definizioni di probabilità (vedere anche su Wikipedia, che propone vari link interessanti). Ma nostante queste possano sembrare delle pessime premesse, nella moderna teoria della probabilità per ricavare il teorema di Bayes sono sufficienti alcune definizioni e pochi passaggi. Ho riassunto gli argomenti trattati in questa parte anche in una presentazione, dal titolo complessità, probabilità e teorema di Bayes. ********************************
Il matematico francese Pierre-Simon Laplace (1749-1827) riscopre ed estende questo risultato in un saggio del 1774, apparentemente ignaro dei risultati di Bayes. Bayes e Laplace rispondono così in linguaggio matematico al vecchio problema di Hume: sorgerà il sole domani? Immaginiamo un alieno che arrivi sulla terra, di notte. L'indomani vede per la prima volta sorgere il sole: quindi lo vede tramontare e scomparire. Chiediamogli che grado di fiducia ripone nel verificarsi dell'evento ricomparsa del sole. Non avendo alcuna altra informazione, la sola risposta ragionevole è 1/2: la probabilità che sorga, e la probabilità che non sorga, sono per lui, a priori, uguali. Ma l’indomani vede il sole sorgere una seconda volta. Quindi il terzo giorno lo vede sorgere ancora, e così via. Chiediamogli ogni volta che grado di fiducia ripone nel verificarsi dell'evento ricomparsa del sole. La soluzione, dopo n giorni, è P = (n+1) / (n+2) (5.1) mentre più in generale per il problema dell’urna contenente s palline dalla quale estraiamo n palline di cui k sono di colore rosso la probabilità che la prossima pallina sia rossa è P = (k+1) / (n+2) (5.2) I due fatti notevoli sono che la probabilità P non dipende da s, e che il valore di P tende a 1 ma non potrà mai raggiungere esattamente tale valore. Quindi l’induzione non potrà mai essere certa. Si consideri uno schema come il seguente, nel quale C rappresenta una delle tante cause osservabili, E rappresenta uno dei tanti effetti osservabili, e le frecce dirette dalla causa all’effetto rappresentano i rapporti di causa/effetto. Il problema classico può essere risolto applicando la deduzione. Conoscendo le cause, possiamo da queste dedurre gli effetti corrispondenti. La soluzione del problema inverso, ovvero l’induzione, è oltremodo più difficile, in quanto ad un effetto possono corrispondere più cause. Il teorema di Bayes consente, a partire dagli effetti osservati, di calcolare la verosimiglianza delle cause, espressa ovviamente nell’unico modo possibile: in termini di probabilità. Fatte queste premesse di tipo epistemologico e di tipo storico, è possibile affrontare l’argomento. Per scoprire subito che, sempre in onore ai motti di Russel e De Finetti, sono oggi ben quattro le definizioni di probabilità (vedere anche su Wikipedia, che propone vari link interessanti). Ma nostante queste possano sembrare delle pessime premesse, nella moderna teoria della probabilità per ricavare il teorema di Bayes sono sufficienti alcune definizioni e pochi passaggi. Ho riassunto gli argomenti trattati in questa parte anche in una presentazione, dal titolo complessità, probabilità e teorema di Bayes. ******************************** |
|
|
|
|
|
||
|
||
|
|
|
|
Ultimo aggiornamento: 20 febbraio 2023
NOTA SUI COLLEGAMENTIALLE FONTI BIBLIOGRAFICHE La maggior parte dei collegamenti ad articoli scientifici riportati nel sito fa riferimento a riviste online che forniscono gratuitamente l’articolo originale. In alcuni casi è necessario registrarsi sul sito per avere libero accesso agli articoli: questo accade per esempio con il BMJ. Quando i collegamenti fanno riferimento a fonti bibliografiche a pagamento, chi non ha sottoscritto un abbonamento con la rivista potrebbe vedere comparire un messaggio del tipo “access forbidden”, ma il più delle volte vedrà comparire una pagina che consente di acquistare online l’articolo originale.
scelti per voi
Programma di statistica Ministat (versione per Windows)
Programma di statistica Open Source R(per Linux, Mac OS X e Windows)
Manuale Merck di diagnosie terapia
L’articolo da non perdere...
Errori congeniti del metabolismo
I migliori libri del mese Leonard Mlodinow La passeggiata dell’ubriaco. Le leggi scientifiche del caso.Rizzoli Editore, 2009, pp. 294ISBN: 17034081
OpenOffice, la suite Open Source (per Linux, Mac OS X e Windows)
ebooks... Mauss, Berg, Rockstroh, Sarrazin, Wedemeyer.Hepatology - A clinical textbook. 10th Edition - 2020
Le lettureconsigliate
Atlante di anatomia del Bock
Tavole metaboliche
Informazioni: info@bayes.itScrivimi: webmaster@bayes.it
NOTA LEGALE L’interpretazione dei risultati delle analisi di laboratorio deve essere effettuata esclusivamente dal medico e alla luce dei dati clinici.Questo sito ha uno scopo esclusivamente educativo e formativo. Pertanto le informazioni in esso contenute possono essere utilizzate esclusivamente a scopo didattico, e anche in questo caso sotto la responsabilità personale di chi le utilizza, sia per sé stesso sia per terzi.Le informazioni contenute in questo sito non possono e non devono essere utilizzate né a scopo diagnostico, né a scopo prognostico, né a scopo terapeutico, né per qualsiasi attività che abbia un impatto sia diretto sia indiretto sullo stato di salute di un individuo o di più individui.Nessuna responsabilità può essere imputata all’autore per danni diretti o indiretti e di qualsivoglia natura che potrebbero essere causati a sé stessi o a terzi a causa di errori, imprecisioni, omissioni, interpretazioni o utilizzo dei contenuti di questo sito o dei siti cui esso fa riferimento.
E ora che i test genetici sono alla portata di tutti?Con meno di mille euro è possibile comprare un test genetico su Internet: si manda un piccolo campione di cellule e poi si aspetta la risposta. Ma... a che cosa serve la risposta? Un dossier di Marika De Acetis dall’Archivio storico del sito www.torinoscienza.it
[Home] [Errori cognitivi] [Epistemologia] [Teorema di Bayes] [Decisioni mediche] [Le basi biochimiche][Analisi tradizionali] [Analisi genetiche] [Qualità in laboratorio] [Statistica e laboratorio][Storia delle medicina] [Download] [Link] [Bacheca] [FAQ] [Chi sono]
Attualità in tema di eGFR:
I migliori libri del mese Giovanni Federspil Logica clinica. I principi del metodo in medicina.McGraw-Hill, 2004, pp. 368ISBN: 88 386 2984-6
Atlante di virologia
Dal settembre 2008oltre 400 000 visitatori
ebooks... M. BesozziErrori cognitivi, probabilità e decisioni mediche. Fate click sul titolo o scaricate il testo su tablet o smartphone con il codice a barre riportato qui sotto. 
Atlante dei protozoi intestinali
Atlante di citologia e istologia
Statistica e grafica con R
Espressione dei risultati nel laboratorio di chimica clinica
Pathology outlines
Atlante di anatomia del Gray
Atlante di ematologia
Atlante di parassitologia
Micobatteriologia clinica
Concetti, metodi e strumenti per una
buona informazione
ebooks... M. BesozziStatistica e grafica con R Fate click sul titolo o scaricate il testo su tablet o smartphone con il codice a barre riportato qui sotto. 
I migliori libri del mese Luigi Tesio I bravi e i buoni.Perché la medicina clinica può essere una scienza.Il Pensiero Scientifico Editore, 2015, pp. 216 ISBN: 978-88-490-0538-7
Gli inganni della correlazione:
Storia delle unità di misura
Questo sito è stato archiviato ed è reso disponibile esclusivamente come memoria storica: pertanto è escluso ogni suo possibile utilizzo medico. Le parti del sito riservate al teorema di Bayes rimangono concettualmente valide, ma declino qualsiasi responsabilità per la lenta ma inevitabile obsolescenza dei restanti contenuti dovuta alla comparsa di nuove analisi di laboratorio, di progressi nelle analisi genetiche, di link interrotti, e quant’altro.
.